Задача о вычислении площади криволинейной трапеции, приводящая к понятию определённого интеграла
Раздел 10. Определённый интеграл.
1. Задача о вычислении площади криволинейной трапеции, приводящая к понятию определённого интеграла.
2. Определение определённого интеграла, его свойства.
3. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
4. Замена переменной в определённом интеграле.
5. Интегрирование по частям в определённом интеграле.
6. Несобственные интегралы. Несобственный интеграл I рода.
7. Признаки сходимости несобственных интегралов I рода.
Задача о вычислении площади криволинейной трапеции, приводящая к понятию определённого интеграла.
Необходимо вспомнить историю и заметить, что ко времени появления понятия интеграла в трудах Ньютона и Лейбница, математика, механика и физика добились выдающихся достижений. К примеру, были рассчитаны траектории планет солнечной системы. В частности, самая дальняя планета Плутон ещё не была увиденной астрономами, а её траектория была рассчитана. Говорили, что Плутон был открыт «на кончике пера». При этом, по нынешней терминологии, школа Ньютона развивала неопределённый интеграл.
Вместе с тем, в геометрии «зияла дыра», смущавшая умы математиков целые столетия - математики и в XVIII веке умели вычислять площади фигур, как и древние греки, т.е. площади фигур, ограниченных отрезками прямой. Из криволинейных фигур известна была лишь площадь круга. Площадь под параболой y= 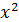 ,например, на отрезке [0,1],вычислить не могли. Эту задачу впервые удалось решить Лейбницу. Его способ рассуждений оказался универсальным, с его помощью решаются многочисленные прикладные и теоретические задачи и в настоящее время.
,например, на отрезке [0,1],вычислить не могли. Эту задачу впервые удалось решить Лейбницу. Его способ рассуждений оказался универсальным, с его помощью решаются многочисленные прикладные и теоретические задачи и в настоящее время.
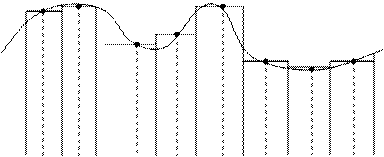
 Итак, требуется вычислить площадь фигуры, ограниченной снизу осью ОХ (т.е. прямой y=0),сверху кривой y=f(x) и по бокам прямыми x=a и y=b (рис.1).Такая фигура называется криволинейной трапецией.
Итак, требуется вычислить площадь фигуры, ограниченной снизу осью ОХ (т.е. прямой y=0),сверху кривой y=f(x) и по бокам прямыми x=a и y=b (рис.1).Такая фигура называется криволинейной трапецией.
у
 |
 0
0
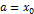
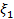
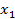
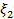
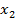
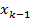
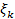
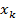
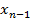
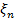
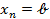
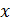
Рис. 1
Вот схема рассуждений Лейбница:
1) Отрезок [a,b] разобьём произвольным образом на n частей точками
a= 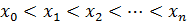 =b и проведем прямые x=
=b и проведем прямые x= 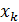 ,к=1,…,n - 1. Этими прямыми фигура разобьётся на n полос. Длину
,к=1,…,n - 1. Этими прямыми фигура разобьётся на n полос. Длину 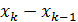 отрезка [
отрезка [ 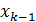 ,
, 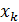 ] обозначим
] обозначим 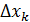 .
.
2) Внутри каждого отрезка [ 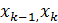 ] возьмём произвольную точку
] возьмём произвольную точку 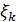 и проведем прямые x=
и проведем прямые x= 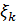 до пересечения с кривой
до пересечения с кривой 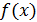 (штриховые линии на рис.1), т.е. вычислим f(
(штриховые линии на рис.1), т.е. вычислим f( 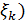 . На каждом отрезке
. На каждом отрезке 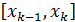 построим прямоугольник с высотой f(
построим прямоугольник с высотой f( 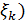 . В результате получим ступенчатую фигуру (рис.1).
. В результате получим ступенчатую фигуру (рис.1).
3)Часть полученной ступенчатой фигуры выступает за пределы криволинейной трапеции, часть, наоборот, находится внутри. Обозначим искомую площадь криволинейной трапеции через S,а площадь ступенчатой фигуры, состоящей из прямоугольников, через 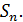
Ясно, что 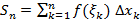 , поэтому имеем приближенное равенство
, поэтому имеем приближенное равенство
S 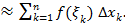 (1)
(1)
Интуитивно ясно, что формула (1) тем точнее, чем больше n и чем меньше
max 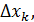 а точное равенство получим в пределе:
а точное равенство получим в пределе:
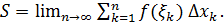 (2)
(2)