Задачи корреляционного анализа

1. Определение формы связи между факторными и результативными признаками (выбор математического уравнения зависимости).

Пример:.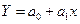

2. Определение параметров математического уравнения (а0, а1,…аn).

3. Оценка тесноты связи между факторными и результативными признаками.

4. Оценка качества полученного уравнения (модели).

Способы выбора формы связи между факторными
и результативными признаками

1. Путем теоретического анализа взаимосвязи между изучаемыми признаками.

2. При помощи аналитической группировки.

3. Графическое изображение показателей (графический анализ).

Пример: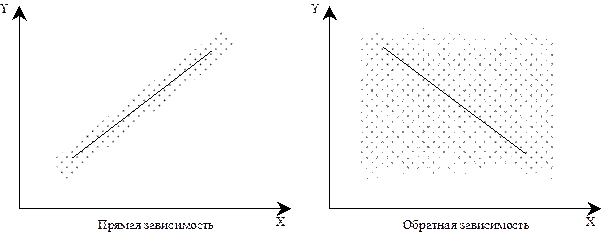

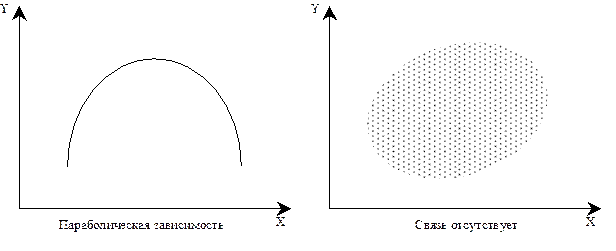
Рис. 7

4. Графическое изображение корреляционной таблицы.

Пример: график зависимости между стоимостью основных фондов (х) и реализацией путевок (y) отелями.

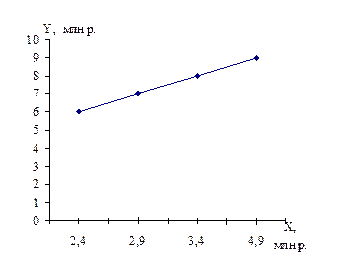
Рис. 8

Парная корреляционная зависимость и ее виды

Парной называется корреляционная зависимость между двумя признаками.

Виды парной корреляционной зависимости (к.з.)

Линейная .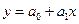

Параболическая .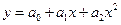

Гиперболическая .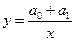

Степенная .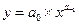

Показательная .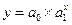

Пример изучения парной линейной корреляционной зависимости.

Имеются данные о реализации путевок (РП) и стоимости основных фондов (ОФ) по 10 отелям.

Этап 1. Определение формы связи между х и у графическим способом (графическое поле корреляции).

№ отеля	Стоимость ОФ, млн р.(х)	РП, (у), млн р.		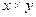х2
		2,4	14,4
		4,0	32,0
		3,6	32,4
		4,0	40,0
		4,5	45,0
		4,6	50,6
		5,6	67,2
		6,5	84,5
		7,0	98,0
		5,0	75,0
Итого	108	47,2	539,1	1236

Графический анализ позволяет сделать вывод о наличии прямой зависимости между x и y вида .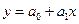

Этап 2. Определение параметров линейного уравнения.

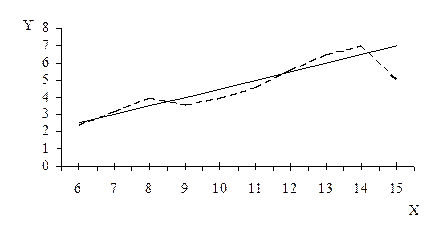
Искомой прямой является такая, которая ближе всего, в смысле способа наименьших квадратов, расположена к точкам, отражающим фактическое распределение явления.

.

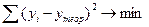Для этого следует решить следующую систему уравнений:

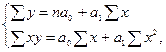
где n – число единиц наблюдения; n=10.

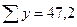
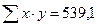
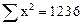
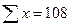
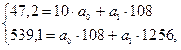
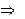
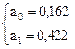
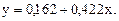
Параметр а1показывает, на сколько единиц в среднем изменится результативный фактор при изменении факторного на единицу. (Пример: при увеличении стоимости на ОФ на 1 млн р. РП увеличится в среднем на 0,424 млн р.)

Параметр а0экономического смысла не имеет.

Системы уравнений для определения параметров
других парных зависимостей

1. Параболическая

Пример: зависимость между возрастом рабочих и их производительностью труда.

.

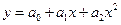
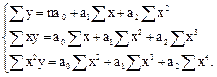2. Гиперболическая

Примеры гиперболической зависимости: зависимость между выпуском продукции (ВП) и себестоимостью; между удельным весом издержек обращения и товарооборотом.

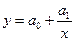
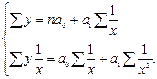
3. Степенная зависимость

Пример: между фондом оплаты труда и выпуском продукции.

.

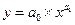
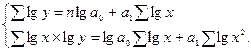4. Показательная зависимость

Пример зависимости между средним доходом на 1 человека и затратами на потребление продуктов питания.

,

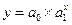
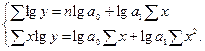Множественная корреляция

Если на результативный фактор (у) воздействует много факторов, то такая корреляция называется множественной.

.

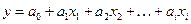Параметры а0, а1, а2,…аi определяются методом наименьших квадратов.

Пример: имеются данные зависимости потребления мяса на одного члена семьи в месяц от среднедушевого дохода и числа членов семьи.

.

№ семьи	Ср. доход в дом на 1 чел. (х)	Число членов (z)	Потребление мяса на 1 чел. (у)	х×у	z×y	х×z	x2	z2	yрасч.
			3,0	210,0	12,0				3,0373
			3,3	280,5	13,2				3,5788
			4,2	378,0	12,6				4,0149
			5,0	500,0	15,0				4,6315
			4,5	562,5	9,0				5,5340
			6,8	1020,0	13,6				6,4365
			6,2	806,0	6,2				5,9701
			7,0	1120,0	7,0				7,0541
Итого:	910	20	40,0	4877,0	88,6	2030	110850	60	40,0257

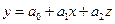
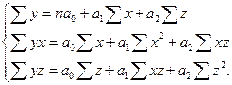
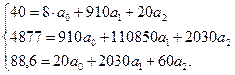
Откуда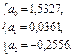

у=1,5327+0,0361х-0,2556z.

Расчетное значение у1=1,5327+0,0361´70-0,2556´4=3,0373 кг.

Параметр а1показывает, что с увеличением дохода на одного члена семьи на 1 р., потребление мяса возрастает в среднем на 0,0361 кг.

Параметр а2показывает, что с увеличением числа членов семьи на одного человека потребление мяса снижается на 0,2556 кг.

Параметр а0экономического смысла не имеет.