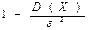Свойства нормального распределения

1. Вероятность попадания случайной величины X, распределённой по нормальному закону, в интервал [х₁, х₂], равна

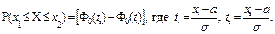
2.Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания a не превысит величину D> 0 , равно:

Р(½Х -а½£D) = 2Ф₀ (t), t = Ds.

По этой формуле можно рассчитать вероятности Р(½Х -а½£D), для различных значений D:

— D = s, Р(½Х -а½£D) = 2Ф(1)=0,6827;

— D = 2s, Р(½Х -а½£D) = 2Ф(2)=0,9545;

— D = 3s, Р(½Х -а½£D) = 2Ф(3)=0,9973.

Экспоненциальный закон распределения вероятностей. Функция надежности

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

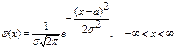
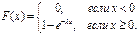функция распределения вероятностей имеет вид:

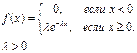
График:

Вероятность попадания случайной величины в интервал (а;в) находится по формуле:

P ( a<X<b) = -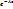

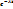
Для показательного распределения:

M(X)= 1/λ

D(X)= 1/

σ(X) = 1/λ

Ф-ция надежности

Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению

R(T) = P( T>t) – вероятность безотказной работы некоторого устройства за время t:

Показательный закон надежности – R(T)= 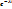,λ-интенсивность отказов. Функция R(T)называется функцией надежности

Двумерные случайные величины. Условные законы распределения составляющих системы дискретных и непрерывных случайных величин

Пусть(Х,У)- двумерная случайная величина, тогда ее распределение можно представить в виде табл. распределения, в каждой клетке (i,j), которой располагается вероятность произведения событий

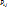= P(X=xi,Y=yj)

Условным законом распределения одной из составляющих двумерной дискретной случ. величины (X,Y) называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенные значения.

Пусть дана двумерная дискретная случ.величина (X,Y)

X1,x2 …xn;y1,y2…yn

Будем обознач.условные вероятности составляющей X

P(xi/yi) (i= 1,2…n;j= 1,2…n)

Условным распределением составляющей Xпри Y=yiназывают совокупность условных вероятностей p(x1/yj), p(x2/yj),…p(xi/yj), вычисленных в предположении, что событиеY=yi уже наступило

Зная закон распределения двумерной дискретной случайной величины, можно вычислить условные законы составляющей

Условные законы распределения составляющей X определяется соотношением:

P(xi/yj)= P(xi/yj)/P(yj)

P(yj/xi)= P (xi/yj)/ P(xi)