Необходимое условие Вейерштрасса сильного минимума

Итак, пусть у нас имеется функционал вида:

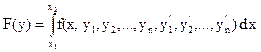
т.е. функционал зависит от независимой переменной x и 2 n функций:

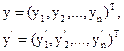
Определим функцию Вейерштрасса

E(x,y,y¢,r)

как функцию 3n+1 переменной следующего вида (3 вектора - y, y¢ и r):

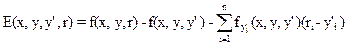
Теорема (Вейерштрасса). Пусть функция ỹ(x) сообщает функционалу F(y) сильный относительный минимум, тогда функция Вейерштрасса на этой экстремали неотрицательна при любом векторе r и для всех x

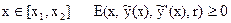
Понятие сильный относительный минимум подразумевает более широкий класс экстремалей, - негладких экстремалей, т.е. экстремали с угловыми точками.

Доказательство.

Пусть точка x₀ – произвольная точка сегмента: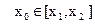

Предположим обратное:

,

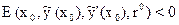при некотором векторе r⁰.

Построим семейство вспомогательных функций вида:

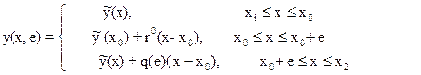
где q(e) – некоторая функция параметра е, который можно выбрать таким малым, чтобы было:

Рассматривая вспомогательную функцию у(х,е) в точке х₀ + е получим:

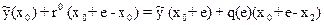
Откуда следует:

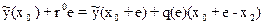
Отсюда видим, что функция q должна выбираться таким образом, что при e=0,

q(0)=0

Продифференцируем вспомогательную функцию у(х,е) по параметру е. Получим:

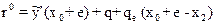, где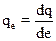

Помня, что 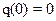получим для q_е в точке 0:

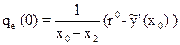
Рассмотрим приращение функционала F(y) для вспомогательной функции (здесь играющей роль функции сравнения) y=y(x,e), предварительно заметив, что y= ỹ(x) на промежутке [x₁,x₀] по самому построению функции у(х,е).

Итак:

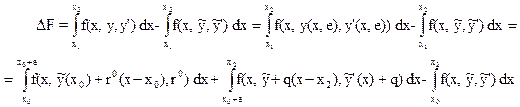
Теперь рассмотрим зависимость приращения функционала от параметра е, т.е. найдем производную:

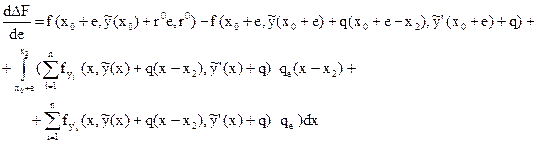
Выбрав е=0 легко заметить, что 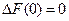, то есть сама производная здесь такова:

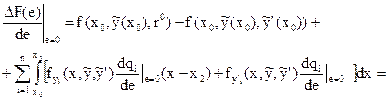
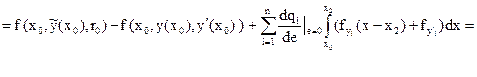
(Интегрируем по частям второе слагаемое в интеграле)

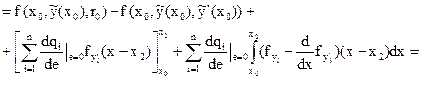
(Но второе слагаемое есть уравнение Эйлера, которое на экстремали обращается в ноль!)

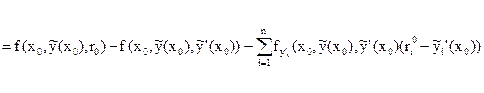
Но ведь полученное выражение есть не что иное, как выражение для функции Вейерштрасса!

Итак, имеем:

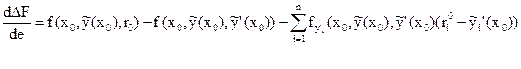
По нашему предположению

,

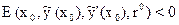а это означает, что

,

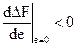при DF(0)=0.

Таким образом, получаем противоречие, - нашли функцию, на которой функционал «меньше минимума»!

Итак

Е (х, у(х), у'(х), r) ³ 0

На экстремали у(х), причем для любых значений вектора r.

В чем смысл неравенства Вейерштрасса!?

Здесь нужно отметить следующие обстоятельства:

1) мы расширили класса экстремалей до таких, которые не принадлежат классу С[x₁,x₂], т.е. предполагаем, что допустимые кривые могут иметь изломы, т.е. точки разрыва производных, иначе говоря расширили постановку вариационной задачи;

2) это обстоятельство как раз и подчеркивается тем, что вектор - параметр r может быть любым, именно он и характеризует величины скачков производных у допустимых кривых;

3) неравенство Вейерштрасса дает нам необходимое условие сильного минимума, оно введено Вейерштрассом именно для класса более широкого, чем гладкие функции, - для класса функций имеющих изломы на промежутке;

4) отметим, что вариации, рассмотренные в доказательстве носят название игольчатых (рис. при n=1)