Краткие теоретические сведения. У многих практических задач необходимо исследовать зависимость режима работы цепи от различных переменных параметров (или от одного из них)

У многих практических задач необходимо исследовать зависимость режима работы цепи от различных переменных параметров (или от одного из них). Например, используя схему замещения трансформатора, можно определить, как будут изменяться токи первичной и вторичной обмотки, снижение напряжения на вторичной обмотке, потеря мощности в трансформаторе и т.д. при изменении сопротивления по характеру и величине в широких диапазонах. На рисунке 60 приведена схема электрической цепи для построения круговой диаграммы.

Рисунок 60 – Схема электрической цепи для построения круговой диаграммы

При этом все переменные величины изображают в комплексной форме, тогда геометрическое место комплексов (векторов) переменных величин представляют в виде годографа или в виде прямой, либо в виде окружности или ее части – дуги. В данной работе буду использованы диаграммы, на которых годографы переменных величин изображаются в виде дуги окружности. Для построения круговых диаграмм необходимо знать способ построения окружности по заданной хорде и вписанным углом, а также уравнением дуги окружности в векторной форме.

Рассмотрим построение круговой диаграммы тока, напряжения и коэффициента мощности для цепи с двумя последовательно соединенными сопротивлениями.

В цепи (рис.60) сопротивление z₁ = 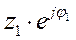– постоянное, а z₂ = 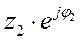изменяется по модулю, угол φ₂ остается неизменным по величине и по знаку.

Уравнение для тока этой цепи – İ = 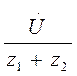, разделим числитель и знаменатель правой части на z₁:

İ = 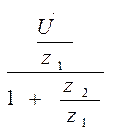= 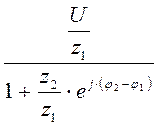. (12.1)

Отношение 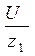= İ_к = İ_к е^j·Ψ·к – ток короткого замыкания цепи, где Ψ_К = Ψ_u – φ₁. Обозначив φ_{2 –} φ₁ = Ψ, получим уравнение дуги круга для тока:

İ = 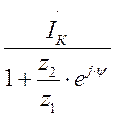(12.2)

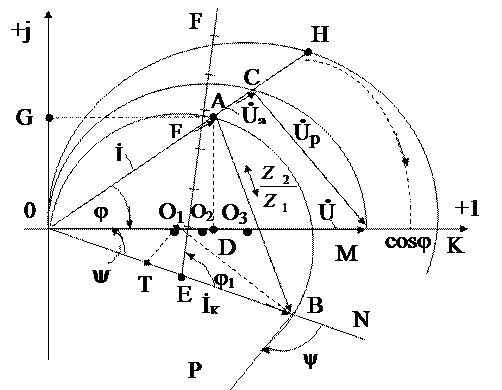
Из этого уравнения видно, что при построении круговой диаграммы тока в качестве хорды берется вектор тока короткого замыкания, а вписанный угол Ψ определяется как разница аргументов переменного и постоянного сопротивлений. Построена по хорде тока короткого замыкания İ_к и вписанному углу Ψ дуга окружности, будет круговой диаграммой для тока İ. Последовательность ее построения может быть предложена следующим образом. Пусть напряжение цепи Ù = Ue^j·0º = U, тогда начальная фаза тока короткого замыкания при z₂ =0; Ψ_К = Ψ_u –φ₁= – φ₁ (смотри рис. 61).

Под углом (– φ₁) проводим линию ОN и на ней в масштабе тока откладываем вектор тока короткого замыкания İ_к. К его продолжению в т.В под углом Ψ проводим касательную РБ. Центр круга О₁ находится на пересечении перпендикуляров О₁Т и О₁В – к средине хорды ОВ.

Пусть отрезок ОА на круговой диаграмме в масштабе тока (m_i = 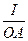) представляет ток I в цепи при каком-либо значении переменного сопротивления. Представим уравнения (11.2) в форме

İ_к = İ + İ· 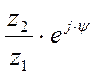. (12.3)

Последнее уравнение показывает, что отрезок АВ в масштабе токов представляет собой İ 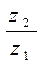. На рисунке 61 представлена круговая диаграмма тока İ, активной составляющей напряжения U_a и cosφ.

Рисунок 61 – Круговая диаграмма тока I, активной составляющей напряжения U_a и cosφ

На линии хорды ОВ отложим отрезок ОЕ в масштабе сопротивлений, тогда линия EF, проведенная под углом (- φ₁) к отрезку ОЕ, и есть линией переменного сопротивления_. Приведем доказательства. Треугольники ОАВ и ОЕF подобны, так как имеют одинаковые углы. Угол АОВ и FОЕ общие, углы АОВ и FЕО равны как углы, и в сумме с вписанным ψ составляют 180⁰, а следовательно, равны и углы АВО и ОFЕ. Из подобия треугольников мы имеем: 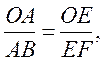откуда EF = 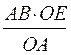, с учетом масштабов токов и сопротивлений:

EF = 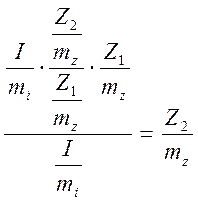. (12.4)

Отрезки ОД и ОG в масштабе мощностей представляют, соответственно, активную и реактивную потребляемую мощности:

P = OD·m_p = OD·U·m_i = OD·U· 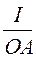= U·I·cosφ, (12.5)

Q = OG·m_p = OG·U·m_i = OG·U· 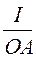= U·I·sinφ, (12.6)

где φ – угол сдвига фаз между током и напряжением цепи.