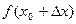Основные правила дифференцирования.

Дифференциальное исчисление.

§1. Понятие производной функции.

Пусть функция 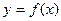определена и непрерывна на промежутке X.

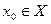Возьмем точку . Дадим аргументу x приращение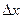 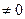так, чтобы 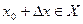. Тогда функция получит приращение .

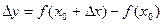Опр. Производной функции 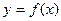в данной точке называется предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю (если этот предел существует):

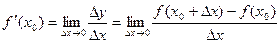
Производную функции обозначают также 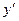, 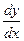. Нахождение производной функции называется дифференцированием этой функции.

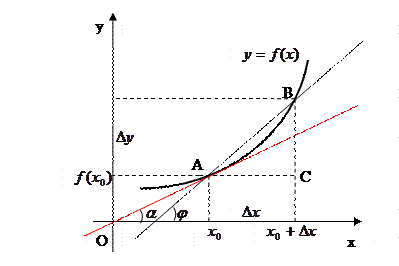
Выясним геометрический смысл производной. Проведем секущую АВ. Из следуют соотношения: .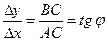

При 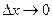точка В будет двигаться по дуге к т. А, и секущая АВ будет стремиться к положению касательной, т.е.

,

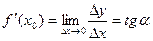где 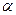- угол между касательной к графику в т. 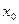и положительным направлением оси Ох. Таким образом, в геометрическом смысле производная функции в точке представляет собой угловой коэффициент (тангенс угла наклона) касательной, проведенной к графику функции в этой точке.

Пример 1.Найти производную функции у=х.

Решение. Для любой точки 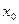найдем производную:

.

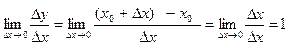Пример 2. Найти производную функции .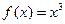

Решение. Для любой точки 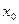найдем производную:

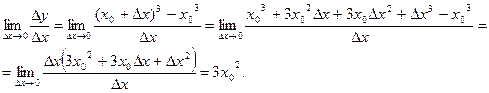
Аналогично можно найти производные всех основных элементарных функций.

Производные основных элементарных функций.

Функция	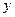Производная	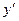	Функция	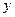Производная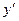
C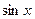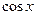

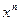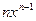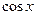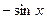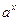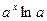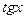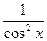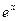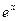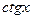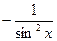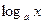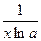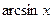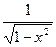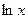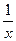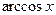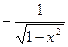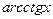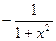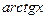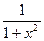Дифференцируемость функции.

Опр. Числовая функция y=f(x) называется дифференцируемой в точке 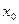, если ее приращение в этой точке можно представить в виде:

,

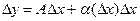где А – некоторое число, 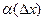- функция от 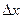, являющаяся бесконечно малой при .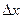

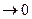Утв. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Теорема1 (о связи между непрерывностью и дифференцируемостью).

Если функция дифференцируема в точке, то она непрерывна в этой точке.

Док-во. Пусть функция y=f(x) дифференцируема в точке 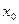. Тогда, по определению, ее приращение можно представить в виде 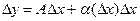. Переходя в этом равенстве к пределу при 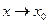, получим:

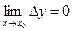, что соответствует определению непрерывности функции.▲

Теорема 1 является необходимым (но не достаточным) признаком дифференцируемости функции в точке. Обратная теорема, вообще говоря, не верна, т.е. если функция непрерывна в точке, то она не обязательно дифференцируема в этой точке.

Пример.

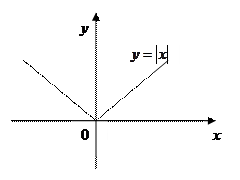Рассмотрим функцию 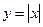, непрерывную в нуле. Докажем, что функция не дифференцируема в т. х=0.

;

.

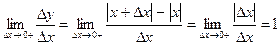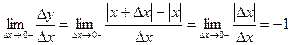Т.к. односторонние пределы в нуле не равны, предел 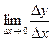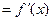не существует.

Основные правила дифференцирования.

1. Производная алгебраической суммы конечного числа дифференцируемых функций равна сумме производных этих функций:

.

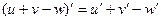2.Производная произведения двух дифференцируемых функций равна сумме произведения производной первого множителя на второй множитель и произведения первого множителя на производную второго:

.

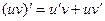Следствие 1. Постоянный множитель можно вынести за знак производной: .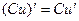

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные:

.

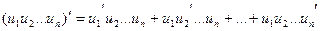3.Производная частногодвух дифференцируемых функций может быть найдена по формуле: ( ).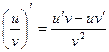

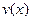
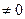Докажем, например, правило 2 (правила1-3 докажите самостоятельно).

Рассмотрим функцию 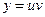. Дадим аргументу 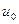приращение 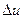, аргументу 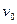приращение 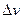. Соответственно, их произведение получит приращение

.

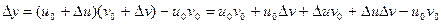Составим отношение 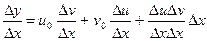. Переходя в этом равенстве к пределу при 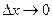, получим:

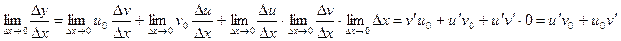
4. Дифференцирование обратной функции.

Если функция 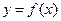имеет обратную функцию 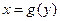и 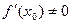, то обратная функция дифференцируема в точке 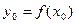, причем

.

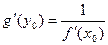5.

Дифференцирование сложной функции.

Если функци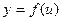и и 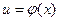дифференцируемы по своим аргументам, то производная сложной функции 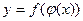существует и равна произведению производной внешней функции по промежуточному аргументу и производной промежуточного аргумента по независимой переменной: .

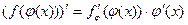Таким образом, производные сложных функций можно вычислить по формулам:

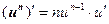
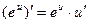
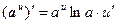
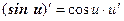
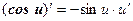
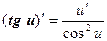
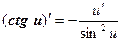
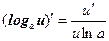
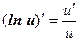
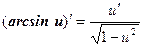
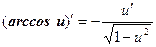
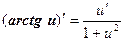
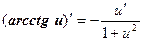
Пример. Найти производную функции 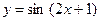.