Процедуры, определенные пользователем

Задача 1

Оценки пяти студентов заносятся в соответствующие массивы из 10 элементов. Массивы заполнить случайным образом. Вывести на экран фамилию студента, среднюю оценку, «Молодец», если она равна или более 7. В противном случае выведи «Подтянись». (Процедуры формирования массива, вывода элементов массива на экран и подсчета средней оценки).

Задача 2

Сформировать 4 массива. Массивы заполнить случайным образом. Вывести на экран исходные массивы и количество положительных элементов в каждом массиве. (Процедуры формирования массива, вывода элементов массива на экран и подсчета количества положительных элементов).

Задача 3

Сформировать 5 массивов. Массивы заполнить случайным образом. Вывести на экран исходные массивы. Удвоить наибольший элемент каждого массива Х(m) и вывести его на экран. (Процедуры формирования массива, вывода элементов массива на экран и нахождения наибольшего элемента массива).

Задача 4

В магазине совершены некоторые покупки. Процедура должна запрашивать цену и количество товара до ввода в цену цифры 0 и посчитать общую стоимость товара.

Задача 5

Написать процедуру для сортировки линейного массива, которая запрашивает, по убыванию или по возрастанию сортировать массивы. Массивы заполнить случайным образом. Отсортировать 3 массива из 20 элементов. Выводить на экран исходные массивы и отсортированные. (Процедуры формирования массива, вывода элементов массива на экран и сортировки массива).

Задача 6

Даны 3 массива из целых чисел. Массивы заполнить случайным образом. Найти элементы этих массивов, которые оканчиваются на 3. (Процедуры формирования массива, вывода элементов массива на экран и проверки, оканчивается ли число на тройку.).

Задача 7

Введите 3 шестизначных номеров троллейбусных билетов – ХХХХХХ. Определите те билеты, номера которых являются «счастливыми», то есть сумма первых трех цифр совпадает с суммой последних трех цифр. Используйте процедуру для определения, является ли номер «счастливым».

Задача 8

Даны стороны основания и высота трех параллелепипедов. Вычислить объем и площади боковой и полной поверхности каждого параллелепипеда по введенным данным.

(Процедура вычисляет объем и площадь поверхности параллелепипеда. Площадь боковой поверхности Sб=Ро*h, где Ро – периметр основания, h – высота. Площадь полной поверхности Sп=Sб+2Sо, где Sо – площадь основания. Объём V=Sо*h)

Задача 9

Вычислить площади трех параллелограммов. Ввести данные: для каждого параллелограмма длину стороны и высоту, проведенную к этой стороне. (Процедура вычисляет площадь параллелограмма. Площадь параллелограмма S=a*h , где a – сторона, h – высота проведенная к этой стороне.)

Задача 10

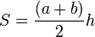Вычислить площади трех трапеций. Ввести данные: для каждой трапеции: a и b – основания и h – высота.

(Процедура вычисляет площадь трапеции. Формула площади трапеции , где a и b – основания и h – высота.)

Задача 11

Два отрезка на плоскости заданы координатами своих концов. Сравнить длины этих отрезков. Нахождение длины отрезка оформить в виде процедуры пользователя.

Задача 12

Напишите программу для поиска максимума среди чисел a+b, b+c, a+c. Поиск максимума из 3 чисел оформить в виде процедуры пользователя. Ввод данных a, b и c организовать с клавиатуры.

Задача 13

Даны 4 круга. Найти их площадь с использованием процедуры, которая производит вычисление и отображает результат на экране. Площадь круга S:=pi*r² .

Задача 14

Пусть дано 3 треугольника, заданных координатами своих вершин. Найдите треугольник с максимальной площадью и выведите эту площадь на экран. Напишите процедуру для нахождения площади треугольника.

Задача 15

Организации требуется красить баки цилиндрической формы. Красят только верхнюю часть и стенки с внешней стороны. Определить, сколько банок краски необходимо для покраски каждого из 3 баков.

Программа должна запрашивать у пользователя следующую информацию для каждого бака: диаметр бака; высота бака; расход краски (площадь поверхности, которую можно покрасить одной банкой краски). При получении дробного числа округление должно всегда происходить в большую сторону.

Площадь крыши бака (круга) вычисляется по формуле Sосн = pi*d2 /4 (где pi – число пи (π), d - диаметр). Площадь боковой поверхности цилиндра: Sбок = p*d*h (где h – высота).