Решение задач раздела I
1.
1) 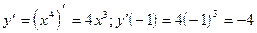
2) 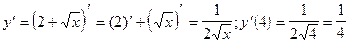
3) 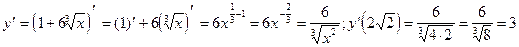
4) 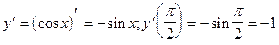
5) 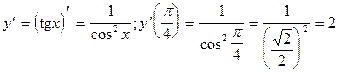
6) 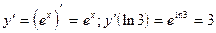
7) 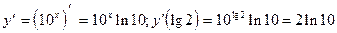
8) 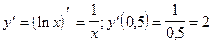
9) 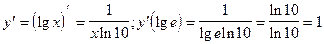
2.
10) 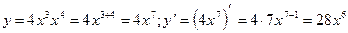
11) 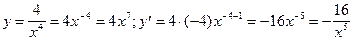
12) 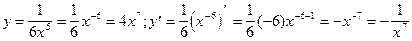
13) 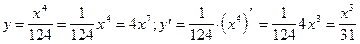
3.
1) 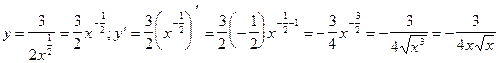
2) 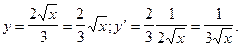
3) 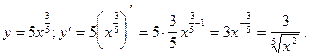
4) 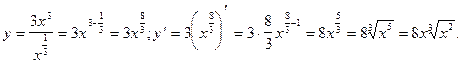
5) 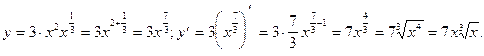
4.
1) 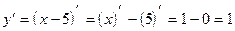
2) 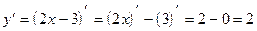
3) 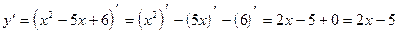
4) 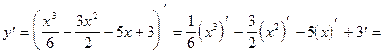
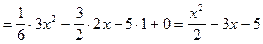
5) 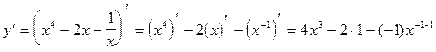
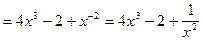
6) 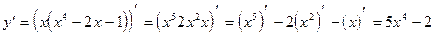
7) 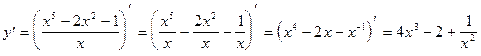
5.
1) 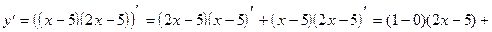
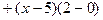
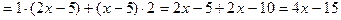
2) 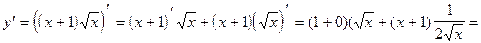
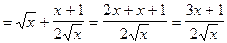
3) 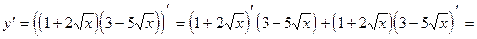
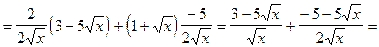
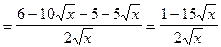
4) 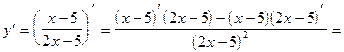
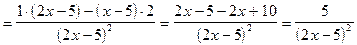
5) 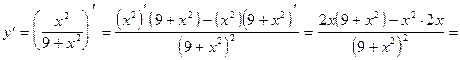
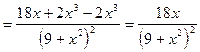
6) 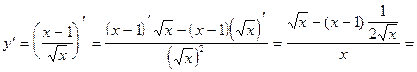
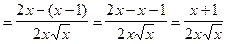
6.
1) 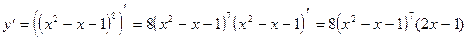
2) 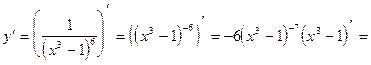
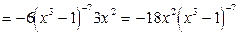
3) 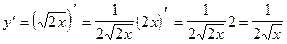
4) 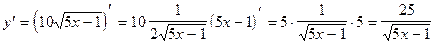
5) 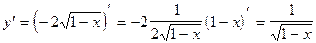
6) 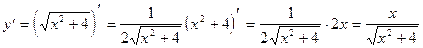
7) 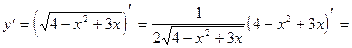
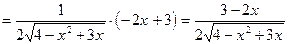
7.
1) О.О.Ф. xÎR; 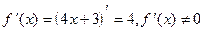 для всех x Î R. Ответ: критических точек нет.
для всех x Î R. Ответ: критических точек нет.
2) О.О.Ф. xÎR; 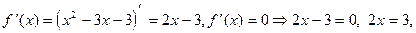
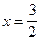 Î О.О.Ф.
Î О.О.Ф.
Ответ: 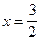 .
.
3) О.О.Ф. xÎR; 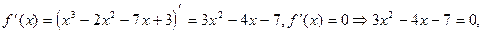 D = 16 + 84 = 100>0;
D = 16 + 84 = 100>0; 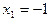 Î О.О.Ф.,
Î О.О.Ф., 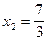 Î О.О.Ф. Ответ:
Î О.О.Ф. Ответ: 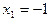 ,
, 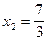
4) О.О.Ф. xÎR; 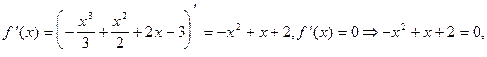
D = 1+8=9>0; 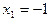 Î О.О.Ф.,
Î О.О.Ф., 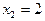 Î О.О.Ф. Ответ:
Î О.О.Ф. Ответ: 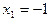 ,
, 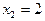
5) О.О.Ф. x¹0; 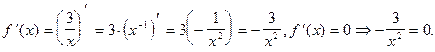
При х = 0 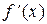 не существует. х = 0 Ï О.О.Ф. Ответ: критических точек нет.
не существует. х = 0 Ï О.О.Ф. Ответ: критических точек нет.
6) О.О.Ф. 2х - х2 ³ 0; х(2-х)³0 Þ 0£ х£ 2.
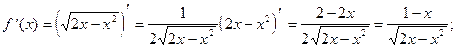
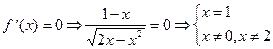
При х = 1 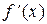 =0. При х = 0 и х = 2
=0. При х = 0 и х = 2 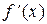 не существует.
не существует.
х1 = 1 Î О.О.Ф., х2 = 0 Î О.О.Ф., х3 = 2 Î О.О.Ф. Ответ: х1 = 1, х2 = 0, х3 = 2.
8.
1) О.О.Ф.: хÎR; 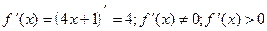 для всех хÎR.
для всех хÎR.
Ответ: возрастает для всех хÎR.
2) О.О.Ф.: хÎR; 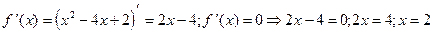 ÎО.О.Ф.
ÎО.О.Ф.
 Ответ: убывает на (-¥; 2)
Ответ: убывает на (-¥; 2)
возрастает на (2; +¥)
3) О.О.Ф.: хÎR; 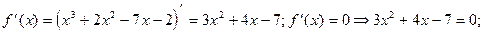 D=16+84=100>0; х1 = -7/3 Î О.О.Ф., х2 = 1 Î О.О.Ф.
D=16+84=100>0; х1 = -7/3 Î О.О.Ф., х2 = 1 Î О.О.Ф.
 Ответ: возрастает на (-¥; -7/3), (1; +¥)
Ответ: возрастает на (-¥; -7/3), (1; +¥)
убывает на (-7/3; 1)
4) О.О.Ф.: х¹ 1; 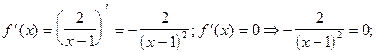
При х = 1 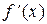 не существует х = 1 ÎО.О.Ф.
не существует х = 1 ÎО.О.Ф.
 Ответ: убывает на (-¥; 1), (1; +¥)
Ответ: убывает на (-¥; 1), (1; +¥)
5) О.О.Ф.: 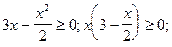 0£х£6.
0£х£6.
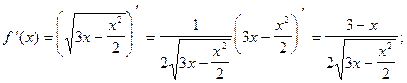
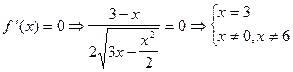
При х = 3ÎО.О.Ф. 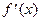 =0. При х = 0ÎО.О.Ф., х = 6ÎО.О.Ф.
=0. При х = 0ÎО.О.Ф., х = 6ÎО.О.Ф. 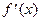 не существует.
не существует.

Ответ: возрастает на (0; 3),
убывает на (3; 6).
9.
1) О.О.Ф.: хÎR; 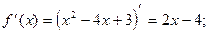
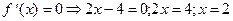 ÎО.О.Ф.
ÎО.О.Ф.

хmin= 2; уmin = y(xmin) = у(2) = 22-4×2+3=4-8+3=-1.
Ответ: хmin= 2;
уmin = -1.
2) О.О.Ф.: хÎR; 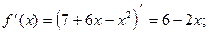
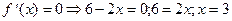 ÎО.О.Ф.
ÎО.О.Ф.

хmax= 3; уmax = y(xmax) = у(3) = 7+6×3-32=7+18-9=16
Ответ: хmax= 3;
уmax = 16
3) О.О.Ф.: хÎR; 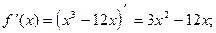
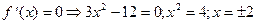 ÎО.О.Ф.
ÎО.О.Ф.

хmax= -2; уmax = y(xmax) = у(-2) = (-2)3-12×(-2)=-8+24=6
хmin= 2; уmin = y(xmin) = у(2) = 23-12×(2)=8-24=-6.
Ответ: хmax= -2; уmax =6
хmin= 2; уmin =-6.
4) О.О.Ф.: хÎR; 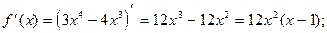
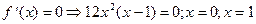 ÎО.О.Ф
ÎО.О.Ф

хmin= 1; уmin = y(xmin) = у(1) = 3×14-4×13=3-4=-1.
Ответ: хmin= 1; уmin =-1.
5) О.О.Ф.: хÎR; 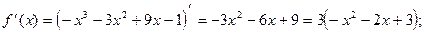
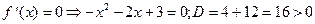 х1 =-3ÎО.О.Ф., х2 =1ÎО.О.Ф
х1 =-3ÎО.О.Ф., х2 =1ÎО.О.Ф

хmin= -3; уmin = y(xmin) = у(-3) = -(-3)3-3(-3)2+9(-3)-1=27-27-27-1=-28;
хmax= 1; уmax = y(xmax) = у(1) = -(1)3-3(1)2+9(1)-1=-1-3+9-1=4.
Ответ: хmin= -3; уmin =-28;
хmax= 1; уmax = 4.
6) О.О.Ф.: х2-2х³0, х(х-2)³0 Þ х Î (-¥; 0] È [2; +¥).
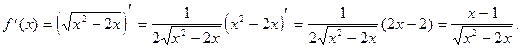
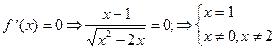
х = 1 Ï О.О.Ф.

Ответ: экстремумов нет.
10.
1) О.О.Ф.: хÎR; 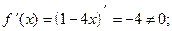 критических точек нет.
критических точек нет.
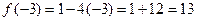 – наибольшее значение
– наибольшее значение
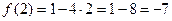 – наименьшее значение.
– наименьшее значение.
Ответ: 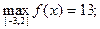
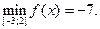
2) О.О.Ф.: хÎR; 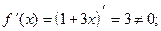 критических точек нет.
критических точек нет.
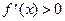 для всех хÎR Þ f(x) возрастает на [-2; 3).
для всех хÎR Þ f(x) возрастает на [-2; 3).
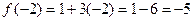 – наименьшее значение.
– наименьшее значение.
Наибольшее значение данная функция не достигает.
Ответ: 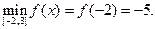
3) О.О.Ф.: хÎR; 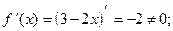 критических точек нет.
критических точек нет.
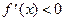 для всех хÎR Þ f(x) убывает на [-1; 2).
для всех хÎR Þ f(x) убывает на [-1; 2).
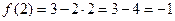 – наименьшее значение.
– наименьшее значение.
Наибольшее значение данная функция не достигает.
Ответ: 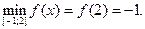
4) О.О.Ф.: хÎR; 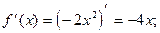
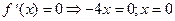 Î О.О.Ф.
Î О.О.Ф.
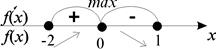
хтах = 0 – единственная точка экстремума.
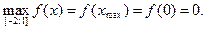
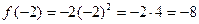 – наименьшее значение;
– наименьшее значение;
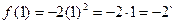
Ответ: 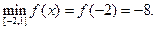
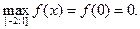
5) О.О.Ф.: хÎR; 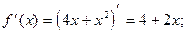
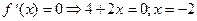 Ï [-1; 0].
Ï [-1; 0].
f(-1)=4×(-1)+(-1)2=-4+1=-3 – наименьшее значение;
f(0)=4×(0)+(0)2=0 – наибольшее значение.
Ответ: 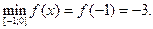
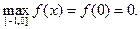
6) О.О.Ф.: хÎR; 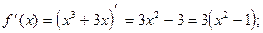
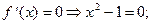 х = 1 Î [0; 3]; x = -1 Ï [0; 3].
х = 1 Î [0; 3]; x = -1 Ï [0; 3].
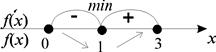
f(1)=1-3=-2 – наименьшее значение;
f(0)=0;
f(3)=27-9=18 – наибольшее значение.
Ответ: 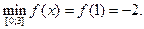
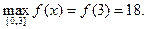
11.
 |
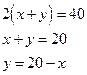
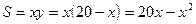
О.О.Ф. площади: 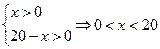 .
.
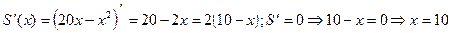 ÎО.О.Ф.
ÎО.О.Ф.
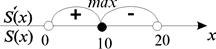
хтах = 10 – единственная точка экстремума.
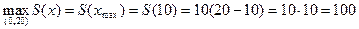
Стороны прямоугольника: х = 10, у = 20-10=10.
Ответ: квадрат со стороной 10.
Ответы к задачам раздела II.
1.
1) 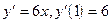 ;
;
2) 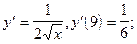
3) 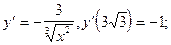
4) 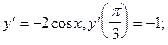
5) 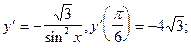
6) 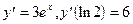 ;
;
7) 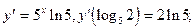
8) 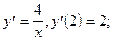
9) 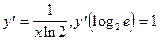 .
.
2.
1) 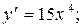 2)
2) 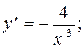 3)
3) 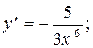 4)
4) 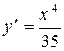 .
.
3.
1) 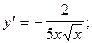 2)
2) 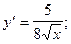 3)
3) 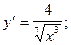 4)
4) 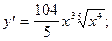 5)
5) 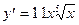 .
.
4.
1) 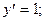
2) 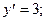
3) 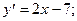
4) 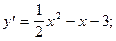
5) 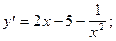
6) 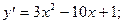
7) 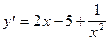 .
.
5.
1) 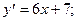
1) 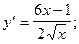
2) 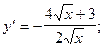
3) 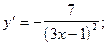
4) 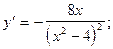
5) 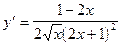 .
.
6.
1) 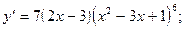
2) 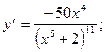
3) 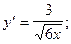
4) 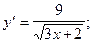
5) 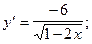
6) 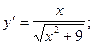
7) 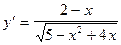 .
.
7.
1) Критических точек нет;
2) {2,5};
3) {-5/3; 1};
4) {-3; 2};
5) критических точек нет;
6) {0; 2; 4}.
8.
1) возрастает на (-¥; +¥);
2) убывает на (-¥; 3),
возрастает на (3; +¥);
3) возрастает на (-¥; -5/3), (1; +¥),
убывает на (-5/3; 1);
4) убывает на (-¥; 2), (2; +¥);
5) возрастает на (-¥; 5),
убывает на (5; +¥).
9.
1) xmin = 3, ymin = -4;
2) xmax = 4, ymax = 25;
3) xmin = -1, ymin = -4,
xmax = 1, ymax = 4;
4) xmin = -1, ymin = -1;
5) xmin = 1, ymin = 2,
xmax = 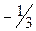 , ymax =
, ymax = 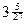 ;
;
6) экстремумов нет.
10.
1) 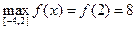 ,
,
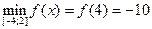 ;
;
2) 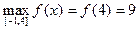 ,
,
наименьшего нет;
3) 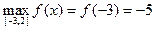 ,
,
наименьшего нет;
4) 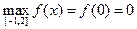 ,
,
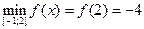 ;
;
5) 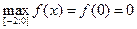 ,
,
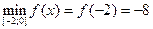 ;
;
6) 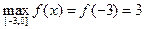 ,
,
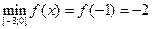 .
.
Квадрат со стороной 9.
