Матрицы. Операции с матрицами
Определение 1.1. Числовой матрицей размера m´n, где m – число строк, n – число столбцов, называется таблица чисел, расположенных в определённом порядке. Эти числа называются элементами матрицы. Место каждого элемента 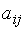 однозначно определяется номером строки i и номером столбца j, на пересечении которых он находится:
однозначно определяется номером строки i и номером столбца j, на пересечении которых он находится:

Иногда коротко пишут  т. е. i меняется от 1 до m, j – от 1 до n.
т. е. i меняется от 1 до m, j – от 1 до n.
Замечание. Матрица размерностью  состоит из одного элемента и равна этому элементу.
состоит из одного элемента и равна этому элементу.
Далее рассмотрим специальные виды матриц.
Определение 1.2. Матрицей-строкой (строчечной матрицей) называется матрица 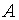 размерности
размерности  , состоящая из одной строки:
, состоящая из одной строки:

Определение 1.3. Матрицей-столбцом (столбцевой матрицей, числовым вектором) называется матрица  размерности
размерности  , состоящая из одного столбца:
, состоящая из одного столбца:

Определение 1.4. Квадратной матрицей порядка 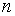 называется матрица, у которой число строк и число столбцов одинаково и равно
называется матрица, у которой число строк и число столбцов одинаково и равно 

Элементы матрицы, расположенные на главной диагонали матрицы, имеют одинаковые индексы строки и столбца: 
Определение 1.5.Единичной матрицей  называется квадратная матрица, у которой все элементы главной диагонали равны единице, а все остальные элементы – нулю:
называется квадратная матрица, у которой все элементы главной диагонали равны единице, а все остальные элементы – нулю:

Определение 1.6. Если в квадратной матрице  , то матрица называется симметричной.
, то матрица называется симметричной.
Пример.  симметричная матрица.
симметричная матрица.
Определение 1.7.Квадратная матрица вида

называется диагональнойматрицей.
С матрицами можно выполнять следующие операции: сложение, умножение на число, умножение матриц, транспонирование.
Определение 1.8. Суммой двух матриц  и
и  одной размерности называется такая третья матрица
одной размерности называется такая третья матрица  той же размерности, что и матрицы–слагаемые, каждый элемент которой
той же размерности, что и матрицы–слагаемые, каждый элемент которой  представляет собой сумму соответствующих элементов матриц
представляет собой сумму соответствующих элементов матриц 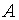 и
и  :
:
 .
.
Определение 1.9. Произведением матрицы  на действительное число
на действительное число  называется такая матрица
называется такая матрица  той же размерности, что и матрица
той же размерности, что и матрица 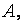 каждый элемент которой
каждый элемент которой  представляет собой произведение соответствующего элемента матрицы
представляет собой произведение соответствующего элемента матрицы 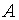 на число
на число  :
:

Пример. Даны матрицы
 ;
;  ,
,
найти матрицу 
Пользуясь определениями 1.8 и 1.9, получим следующие матрицы:


Определение 1.10. Произведением матрицы  размерности
размерности  с матрицей
с матрицей  размерности
размерности  в указанном порядке называется такая третья матрица
в указанном порядке называется такая третья матрица  размерности
размерности  каждый элемент которой
каждый элемент которой  представляет собой сумму произведений соответствующих элементов
представляет собой сумму произведений соответствующих элементов 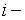 й строки матрицы
й строки матрицы 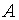 и
и 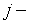 го столбца матрицы
го столбца матрицы  :
:
 .
.
Замечание. Из определения 1.10 следует, что перемножать можно только те матрицы, у которых число столбцов первого множителя равно числу строк второго.
Определение 1.11. Матрица  размерности
размерности  называется транспонированной по отношению к матрице
называется транспонированной по отношению к матрице 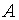 размерности
размерности  , если она получена из неё заменой строк столбцами (или, что то же, столбцов – строками):
, если она получена из неё заменой строк столбцами (или, что то же, столбцов – строками):

Пример. Даны матрицы


Составить матрицу 
Пользуясь определениями 1.10 и 1.11, получим матрицы
 ;
;

Пример. Найти произведение матриц
 и
и  .
.
По определению 1.10, результатом перемножения матриц 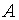 и
и  будет матрица размерности
будет матрица размерности  а при перемножении матриц
а при перемножении матриц  и
и 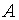 получится матрица размерности
получится матрица размерности 



Пример. Найти произведение матриц
 и
и 
По определению 1.10, результатом перемножения матриц 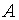 и
и  будет матрица размерности
будет матрица размерности 

Пример. Дана матрица

Записать матрицу 
Воспользуемся определением 1.10 и запишем:



Теорема 1.1.Операции с матрицами обладают следующими основными свойствами:
1.  – коммутативность сложения матриц.
– коммутативность сложения матриц.
2.  – ассоциативность сложения матриц.
– ассоциативность сложения матриц.
3.  – произведение матриц в общем случае некоммутативно.
– произведение матриц в общем случае некоммутативно.
4.  – ассоциативность произведения матриц.
– ассоциативность произведения матриц.
5.  – дистрибутивность умножения матрицы на число относительно сложения действительных чисел
– дистрибутивность умножения матрицы на число относительно сложения действительных чисел 
6.  – дистрибутивность умножения матрицы на действительное число
– дистрибутивность умножения матрицы на действительное число  относительно сложения матриц.
относительно сложения матриц.
7.  – двойное транспонирование матрицы имеет своим результатом исходную матрицу.
– двойное транспонирование матрицы имеет своим результатом исходную матрицу.
8.  если эти произведения имеют смысл.
если эти произведения имеют смысл.
