Автономная система, находящаяся под наблюдением
Лекция 1
Многомерные системы. Основные понятия и определения.
Устойчивость. Управляемость. Наблюдаемость
Основные понятия и определения.
Теория автоматического управления – раздел технической кибернетики, объектом исследования которого являются системы автоматического управления (САУ) различной природы и степени сложности. Теория автоматического управления (ТАУ) разрабатывает принципы построения систем управления и изучает основные закономерности протекающих в них процессов. ТАУ является одной из научных и методологических основ, на базе которых целенаправленно объединяются усилия специалистов различного профиля, участвующих в создании современных сложных САУ. При изучении процессов управления ТАУ абстрагируется от природы и конструктивных особенностей составных частей САУ. Вместо реальных объектов в ТАУ рассматриваются их адекватные математические модели – динамические системы.
Система автоматического управления (регулирования) -комплекс устройств, обеспечивающих автоматическое изменение (стабилизацию) координат объекта управления с целью установления желаемого режима работы объекта.
Модель математическая – система математических соотношений, описывающих изучаемый процесс или явление. Для составления математической модели (ММ) можно использовать любые математические средства, при этом процесс составления ММ называется математическим моделированием. Это самый общий и наиболее употребляемый в науке, в частности в кибернетике и автоматике, метод исследования.
Система динамическая– под динамическими системами понимаются системы различной природы – механические, электрические, биологические и др., процессы в которых отображаются, в основном, дифференциальными уравнениями.
Одномерные системы автоматического управления –автоматические системы, у которых одна управляемая величина (координата) и одно управляющее воздействие.
Многомерные (многосвязные) системы автоматического управления -автоматические системы, у которых число, как управляемых координат, так и управляющих воздействий равно двум и более. Специфика таких систем заключается в том, что поведение каждой управляемой координатой определяется всей совокупностью управляющих воздействий, образующих вектор управления, а также вектором возмущающих воздействий. Необходимость в создании таких систем возникает в тех случаях, когда требуется управлять одновременно несколькими взаимосвязанными параметрами некоторого физического процесса.
1.2 Описание автоматических систем.Линейные автоматические системы могут иметь следующие описания (математические модели).
1.2.1 Автономная система.Математическое описание автономной системы в общем виде следующее
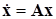, с начальными условиями 
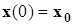. (1.1)
В развернутом виде описание системы (1.1) следующее
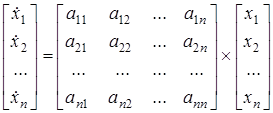. (1.2)
В скалярном виде описание системы (1.1) следующее
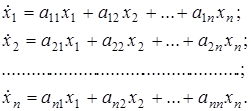(1.3)
Свойства системы определяются ее устойчивостью. Структура системы представлена на рисунке 1.
Автономная система, находящаяся под наблюдением
1.2.2.1 (SO - singl-output).Математическое описание системы в общем виде следующее
, , 
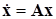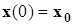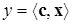. (1.4)
В развернутом виде описание системы (1.4) следующее
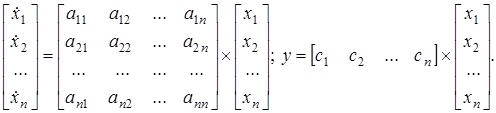(1.5)
В скалярном виде описание системы (1.4) следующее
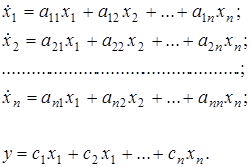(1.6)
Помимо устойчивостидля данной системы существует такое понятие, как свойство полной наблюдаемости. Структура системы представлена на рисунке 2.
1.2.2.2 (MO - multi-output).Математическое описание системы в общем виде следующее
, , 
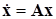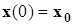. (1.7)
В развернутом виде описание системы (1.7) следующее
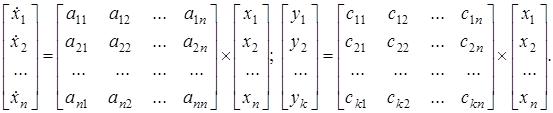(1.8)
В скалярном виде описание системы (1.7) следующее
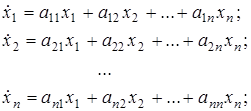
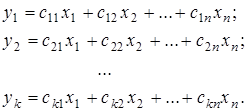(1.9)
Помимо устойчивостидля данной системы существует такое понятие, как свойство полной наблюдаемости. Структура системы представлена на рисунке 3.