В недесяткових системах числення 9 страница
нерівності).
А3. (  а) (
а) (  b) (
b) (  ! с) (с = а + b); а, b, с Є М (існування і єдиність суми).
! с) (с = а + b); а, b, с Є М (існування і єдиність суми).
А4. (  а) (
а) (  b) (а + b = b + а); а, b, Є М (комутативність додавання).
b) (а + b = b + а); а, b, Є М (комутативність додавання).
А5. (  а) {
а) {  b) (
b) (  с)((а+b) + с = а + (b + с)); а, b, с Є М (асоціативність
с)((а+b) + с = а + (b + с)); а, b, с Є М (асоціативність
додавання).
А6. Існує нульова величина (величина, що дорівнює нулю), яку позначають 0.
Вона має такі властивості:
а)(  а) (а
а) (а 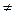 0
0 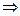 а>0):
а>0):
6)(  а)(а + 0 = а);
а)(а + 0 = а);
в)(  а)(0 ·
а)(0 ·  а = 0);аЄМ;
а = 0);аЄМ;
А7. (  а) (
а) (  b
b 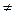 0) (а + b> а); а, b Є М (монотонність додавання).
0) (а + b> а); а, b Є М (монотонність додавання).
А8. (  а) (
а) (  b) (а
b) (а 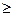 b
b 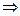 (
( 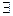 ! с) ( b + с = а); а, b, с Є М (виконуваність
! с) ( b + с = а); а, b, с Є М (виконуваність
віднімання).
А9. (  а) (
а) (  п
п 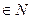 ) (
) ( 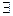 b) (пb = а); а, b ЄМ (виконуваність ділення).
b) (пb = а); а, b ЄМ (виконуваність ділення).
А10. (  а) (
а) (  b>0) (
b>0) ( 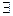 п
п 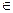 N)(а<пb); а, b ЄМ(аксіома Архімеда).
N)(а<пb); а, b ЄМ(аксіома Архімеда).
А11. Для двох послідовностей величин
a1<а2<аз< ... <bз< b2< b1
завжди існує така величина с, яка більша від усіх ап і менша, ніж усі bп
(аксіома неперервності).
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
1. Курс математики: Навч. посібник /В.Н. Боровик. - К.: Вища шк., 1995. с.
349-355.
2. Теоретичні основи початкового курсу математики: Навч. посібник
ІВМ. Кухар. - К.: Вища шк., 1987. с. 269-274.
3. Л.П. Стойлова. Основи начального курса математики. М.: Просвещение,
1988. с. 277-287.
4. Н.Б. Істоміна. Практикум з методики викладання математики у
початкових класах. М.: Просвещение, 1986. с. 26-27.
 Практичне заняття № 7
Практичне заняття № 7
Тема. Дії з величинами. Модульний контроль
Мета.Застосувати теоретичні відомості про функції, графіки і їх властивості та величини до розв’язування вправ.
Студенти повинні знати:
· поняття величини і її вимірювання;
· величини, що вивчаються в курсі математики 1-4 класів;
· довжина і її вимірювання;
· площа фігури і її вимірювання;
· обєм, його вимірювання і властивості;
· маса тіла, її основні властивості і одиниці вимірювання;
· час, його властивості і одиниці вимірювання;
· вартість та залежність між величинами ціна, кількість, вартість.
Студенти повинні вміти:
· виконувати операції над величинами.
Література
1. Курс математики: Навч. посібник / В. Н. Боровик. – К. : Вища шк., 1995. С. 238 – 287. 349 – 379.
2. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. – К. Вища шк., 1980. С. 153-154, 157-161.
3. Теоретичні основи початкового курсу математики: Навч. посібник / В. М. Кухар. – К. Вища шк., 1987. С. 192 -199.
4. Основы начального курса математики: Учеб. пособие Л. П. Стойлова. - М. “Просвещение” 1988. С. 242 - 307.
План та хід заняття
І. Актуалізація опорних знань
1. Поняття величини і її вимірювання.
2. Величини, що вивчаються в курсі математики 1-4 класів.
3. Довжина і її вимірювання.
4.Площа фігури і її вимірювання.
5.Обєм, його вимірювання і властивості.
6. Маса тіла, її основні властивості і одиниці вимірювання.
7. Час, його властивості і одиниці вимірювання.
8. Вартість та залежність між величинами ціна, кількість, вартість.
ІІ. Розв’язування вправ
1. З’ясуйте, яка залежність існує між величинами, даними в задачі, розв’яжіть задачі:
1) Місткість однієї банки 3 л. Скільки потрібно банок, щоб розлити 6 л соку? 9 л? 12 л? 15 л?
2) В перший день магазин продав 8 однакових портфелів і одержав за них 32 грн. За другий день було продано 6 таких портфелів. Скільки грошей одержали за портфелі другого дня?
3) Велосипедист їхав зі швидкістю 12 км/год і був у дорозі 2 год. Скільки часу потрібно пішоходу, щоб пройти цю відстань зі швидкістю 4 км/год?
2. Розв’яжіть задачі і поясніть, які дії над величинами потрібно виконати в процесі розв’язування задач:
1) На базі було 12680 т бензину. За перший день база відпустила 834 т, а за другий день – в 2 рази менше, ніж в перший, а за третій – на 229 т більше, ніж на другий. Скільки тонн бензину залишилося на базі?
2) Із дерев’яної колоди, яка має форму прямокутного паралелепіпеда, довжина якого 24 см, ширина в 3 рази менше від довжини, а висота 11 см, вирізали куб із ребром 6 см. Знайдіть об’єм частини, яка залишилася.
3) На обробку трьох деталей витратили 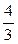 години. На першу деталь було витрачено 0,25 год, на другу
години. На першу деталь було витрачено 0,25 год, на другу 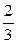 год. Скільки часу витратили на обробку третьої деталі?
год. Скільки часу витратили на обробку третьої деталі?
4) Книжка дешевша альбома на 10 грн. Скільки коштує два таких альбоми, якщо одна книжка коштує 67 грн.?
3. На прямій відмітьте точки А, В, С і D так, щоб відстань від A до B дорівнювало 2 см, відстань від В до С – 1,5 см, від С до D – 1 см. Знайдіть довжини відрізків АВ, AD, BC, CD, якщо за одиничний відрізок прийняти:
1) відрізок CD; 2) відрізок AB; 3) відрізок BC; 4) відрізок AD.
4. Чи існують три точки А, В і С, такі, що:
1) 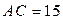 см,
см, 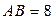 см,
см, 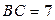 см;
см;
2) 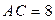 см,
см, 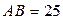 см,
см, 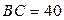 см;
см;
3) 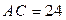 см,
см, 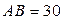 см,
см, 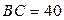 см.
см.
5. Порівняйте величини: 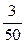 м і
м і 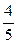 дм.
дм.
6. Відомо, що відстань від пункту А до пункту В дорівнює 6 км, від В до С 8 км. Чому може дорівнювати відстань від А до С?
7. Побудуйте відрізок, довжина якого 4,6е. Яким буде числове значення довжини цього відрізка, якщо одиницю довжини 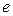 зменшити в 1,5 рази?
зменшити в 1,5 рази?
8. Які дії над довжинами будуть виконувати учні початкових класів при розв’язанні наступних задач:
1) Накресліть квадрат зі стороною 5 см. Знайдіть суму довжин всіх сторін цього квадрата.
2) Сума довжин всіх сторін квадрата дорівнює 28 см. Чому дорівнює довжина сторони цього квадрата?
3) На дитяче простирадло йде 2 м полотна, а на підодіяльник – в 2 рази більше, ніж на простирадло. Скільки полотна необхідно на 8 комплектів, що складаються з одного простирадла і одного підодіяльника?
4) У одному шматку було 24 м тканини, а у другому – на 8 менше. З всієї тканини пошили декілька однакових суконь, використовуючи на кожну по 4 м тканини. Скільки пошили суконь?
5) За три дні турист проїхав 3220 км. За перший день він проїхав четверту частину всього шляху, за другий день 1920 км, а за третій - решту шляху. Скільки кілометрів проїхав турист за третій день?
6) Відрізок довжиною 6 см збільшили в декілька разів і отримали відрізок довжиною 18 см. В скільки разів збільшили відрізок?
9. Чи може прямокутник, довжини сторін якого виражаються ірраціональними числами, бути рівновеликим прямокутнику, довжини сторін якого виражаються числами раціональними?
10. Виконайте дії:
2) від 5 год 36 сек відніміть 45 хв 40 сек;
3) 7 годин 48 хвилин 56 секунд помножте на 18%.
11. Два трикутники мають однакові площі. Чи слідує з цього, що вони рівні?
12. Знайдіть площі фігур, на які накладена палетка (рис. 25), за умови, що довжина сторони квадрата палетки: 1) 1 см; 2) 0,5 см.
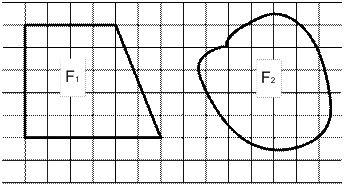
Рис. 25
13. Серед наступних висловлень вкажіть істинні:
1) Числові значення площі однієї і тієї ж фігури можуть бути різними.
2) Числові значення площ нерівних фігур можуть бути рівними.
3) Рівновеликі фігури рівні.
14. Розв'яжіть задачі і поясніть, які операції над площами були при цьому виконані:
1) Площа прямокутника в 3 рази більша площі квадрата. Довжина прямокутника 96 см. Чому дорівнює ширина прямокутника, якщо сторона квадрата 48 см?
2) Загальна площа двох земельних ділянок прямокутної форми дорівнює 7,4 га. Довжина першої ділянки 250 м, довжина другої 150 м. Знайдіть площу кожної ділянки, якщо ширина першої ділянки на 40 м більша ширини другої ділянки.
3) Якщо довжину прямокутника збільшити на 2 дм, а ширину зменшити на 5 дм, то вийде квадрат, площа якого буде менша площі прямокутника на 50 дм2. Визначте площу квадрата.
4) Площа одної стіни кімнати дорівнює 14 м2 90 дм2, а суміжної стіни – 9 м2 80 дм2. В кімнаті є вікно площею 3 м2 50 дм2 і двері 2 м2 20 дм2. Крім того, десята частина стін під стелею не обклеєна шпалерами. Яку площу займають шпалери?
15. Відомий грецький математик Архімед помер в 212 році до нашої ери. Скільки століть і скільки років пройшло з дня смерті Архімеда?
16. В 1956 році виповнилось 2000 років з часу введення юліанського календаря (старий стиль) і 374 роки з часу введення григоріанського календаря (новий стиль). В якому році був введений старий стиль і в якому новий стиль?
ІІІ. Самостійне розв’язування вправ
Тести
Варіант 1
| № п/п | Запитання | Варіанти відповідей |
| Як можна порівняти маси двох предметів, не визначаючи масу кожного з них? | 1. Візуально. 2. Шляхом мускульних зусиль (птримати в руках). 3. Зважити предмети. 4. Шляхом накладання. | |
| Виразіть в міліметрах 8 см 79 мм. | 1. 159 мм. 2. 89 мм. 3. 879 мм. 4. 798 мм. | |
Порівняйте величини: 56 секунд і 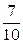 хвилини. хвилини. | 1. 56 секунд = 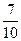 хвилини. 2. 56 секунд > хвилини. 2. 56 секунд > 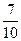 хвилини. 3. 56 секунд < хвилини. 3. 56 секунд < 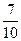 хвилини. 4. Інша відповідь. хвилини. 4. Інша відповідь. | |
| Відстань від дому до школи 400 м, а відстань від дому до вокзалу 0,9 км. У скільки разів відстань від дому до вокзалу більша відстані від дому до школи? | 1. У 2,5 разів. 2. У 1,25 разів. 3. У 0,25 разів. 4. У 2,25 разів. | |
Числове значення довжини відрізка, виміряного за допомогою одиниці 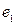 , дорівнює 6, а виміряного за допомогою одиниці , дорівнює 6, а виміряного за допомогою одиниці 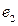 - дорівнює 4. У якому відношенні знаходяться між собою одиниці довжини - дорівнює 4. У якому відношенні знаходяться між собою одиниці довжини 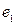 : : 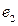 ? ? | 1. 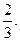 2. 2. 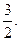 3. 3. 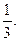 4. 4. 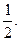 | |
| 13. Площа прямокутника дорівнює 12 см2, довжини його сторін виражаються натуральними числами. Якими натуральними числами неможуть бути виражені сторони прямокутника? | 1. 1 і 12; 2. 2 і 6; 3. 3 і 4; 4. 5 і 7. | |
| Виконайте дії: додайте 5 років 7 місяців 8 днів і 3 роки 2 місяці 4 дні. | 1. 8 років 9 місяців 2 дні. 2. 8 років 9 місяців 12 днів. 3. 8 років 10 місяців 2 дні. 4. 9 років 9 місяців 12 днів. | |
| Площа кухні 9 м2. Скільки плиток лінолеуму, що мають форму квадрата зі стороною 3 дм, необхідно для покриття підлоги на кухні? | 1. 100. 2. 300. 3. 200. 4. 900. | |
| Будівництво будинку було розпочате 12 березня і завершене 7 грудня того ж року. Скільки днів будувався будинок? | 1. 269 днів. 2. 268 днів. 3. 270 днів. 4. 271 день. | |
| Розв'яжіть задачу. З ферми до ремонтної майстерні велосипедист їхав зі швидкістю 12 км/год, а повертався зі швидкістю 15 км/год, тому затратив на зворотний шлях на 18 хвилин менше. Скільки кілометрів від ферми до майстерні? | 1. 18 км. 2. 10 км. 3. 12 км. 4. 15 км. |
Варіант 2
| № п/п | Запитання | Варіанти відповідей |
| Є два шматки дроту. Яким чином можна порівняти їх довжини, не вдаючись до вимірювання? | 1. Візуально. 2. Порахувати. 3. Зважити. 4. Накладанням. | |
| Виразіть в секундах 8 хвилин 12 секунд. | 1. 492 секунди. 2. 812 секунд. 3. 402 секунди. 4. 502 секунди. | |
Порівняйте величини: 1,5 см і 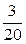 дм. дм. | 1. 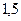 с м = с м = 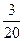 дм. 2. дм. 2. 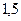 с м = с м = 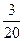 дм. 3. дм. 3. 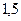 с м = с м = 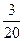 дм. 4. Порівняти не можна. дм. 4. Порівняти не можна. | |
| Довжину столу вимірювали спочатку в сантиметрах, потім в дециметрах. В першому випадку отримали число на 108 більше, ніж у другому. Чому дорівнює довжина столу? | 1. 12 см 2. 120 дм. 3. 12 дм. 4. 1,2 дм. | |
Побудуйте відрізок, довжина якого 4,6е. Яким буде числове значення довжини цього відрізка, якщо одиницю довжини 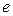 збільшити в 3 рази? збільшити в 3 рази? | 1. 4,6 2. 13,8 3. 27,6 4. 9,2. | |
| Довжини двох нерівних сторін прямокутника виражаються ірраціональними числами. Чи слідує з цього, що значення площі даного прямокутника буде також ірраціональним числом? | 1. Так завжди. 2. Інколи. 3. Ні. 4. Інша відповідь. | |
| Якщо довжину прямокутника збільшити в 2 рази, а ширину зменшити в 2 рази, то площа прямокутника... | 1. Збільшиться в 4 рази; 2. Зменшиться в 4 рази; 3. Не зміниться; 4. Збільшиться в 2 рази. | |
| Виконайте дії: 9 тижнів 21 година 52 хвилини поділіть на 1 тиждень 23 години 44 хвилини. | 1. 7. 2. 8. 3. 6. 4. 9. | |
| Місяць робить повний оберт навколо Землі за 29 днів 12 годин 44 хвилини 3 секунди. Виразіть цей проміжок часу в секундах. | 1. 2551443 с. 2. 2551440 с. 3. 2551441 с. 4. 2551442 с. | |
| Розв'яжіть задачу. Машиністка повинна була передрукувати рукопис за 8 днів. Проте вона виконала роботу за 6 днів, так як друкувала щоденно на 6 сторінок більше, ніж планувала раніше. Скільки сторінок в рукописі? | 1. 144 сторінки. 2. 140 сторінок. 3. 244 сторінки. 4. 104 сторінки. |
ІV. Підсумок. Домашнє завдання
 Практичне заняття № 13
Практичне заняття № 13
|
Мета.Застосувати закони додавання і множення додатних раціональних і дійсних чисел до розв’язування вправ.
Студенти повинні знати:
· означення додатного раціонального числа;
· правила додавання і віднімання раціональних чисел;
· правила множення та ділення раціональних чисел;
· правила виконання дій над дійсними числами та величинами.
Студенти повинні вміти:
· виконувати дії над раціональними числами;
· виконувати дії над дійсними числами та величинами.
Література
1. Пышкало А. М., Стойлова Л. П., Лаврова Н. Н., Ирошников Н. П. Сборник задач по математике. – М.: просвещение, 1979.- С. 189-202.
2. Стойлова Л. П., Пышкало А. М. Основы начального курса математики. – М.: Просвещение, 1988.- С. 219-224.
План та хід заняття
І. Актуалізація опорних знань
1. Означення дробу.
1. Основна властивість дробу.
2. Сума двох дробів (з однаковими і різними знаменниками).
3. Різниця дробів.
4. Добуток дробів.
5. Частка дробів.
8. Закони додавання і множення.
ІІ. Розв’язування вправ
1. На множині дробів 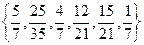 задане відношення рівносильності. Перелічіть всі пари дробів, що знаходяться в цьому відношенні. Побудуйте граф цього відношення.
задане відношення рівносильності. Перелічіть всі пари дробів, що знаходяться в цьому відношенні. Побудуйте граф цього відношення.
2. Дано дріб 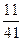 . Яке число треба додати до чисельника і знаменника дробу, щоб отримати дріб
. Яке число треба додати до чисельника і знаменника дробу, щоб отримати дріб 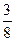 ?
?
3. Обчисліть раціональним способом і поясніть, які закони додавання і множення раціональних чисел при цьому були використані:
а) 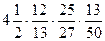
б) 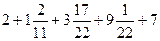 ;
;
в) 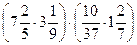 ;
;
г) 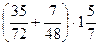 .
.
4. Знайдіть значення виразу:
а) 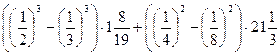 ;
;
б) 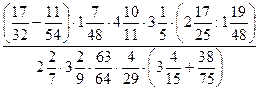 ;
;
5. Серед наступних висловлень вкажіть істинні:
а) 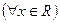 ( х – число ірраціональне);
( х – число ірраціональне);
б) 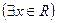 ( х – число раціональне);
( х – число раціональне);
в) 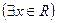 ( х – число ірраціональне);
( х – число ірраціональне);
г) 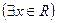 ( х – число ціле);
( х – число ціле);
д) 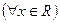 ( х – нескінченний десятковий дріб).
( х – нескінченний десятковий дріб).
6. Відмітьте на координатній прямій точки, що зображують дійсні числа, якщо:
а) 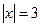 ;
;
б) 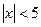 ;
;
в) 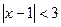 .
.
7. Знайдіть значення числового виразу.
а) 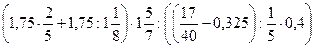 ;
;
б) 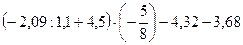
8. Розв’язати алгебраїчним та арифметичним способами задачу:
З пункту А до пункту В велосипедист їхав зі швидкістю 12 км/год, а повертався назад з швидкістю 15 км/год, тому затратив на зворотній шлях на 18 хв менше. Скільки кілометрів від пункту А до пункту В?
9. Розв’язати задачі арифметичним способом і пояснити, які операції над величинами були при цьому виконані.
1) Купили 6 кг 500 г фарби. А фарбування вікон використали п’яту частину всієї фарби, на фарбування кімнати – у 2 рази більше, ніж на фарбування вікон, а на кухню фарби пішло на 800 г менше, ніж на фарбування кімнати. Скільки фарби залишалось?
2) Загальна площа двох земельних ділянок прямокутної форми дорівнює 7,4 га. Довжина першої ділянки 250 м, довжина другої 150 м. Знайти площу кожної ділянки, якщо ширина першої ділянки на 40 м більша, ніж ширина другої.
3) В одному сувої було 24 м тканини, а в другому – на 8 м менше. Із всієї цієї тканини пошили декілька однакових платтів, використовуючи на кожне по 4 м тканини. Скільки пошили платтів?
10. Виконайте дії:
а) додайте 5 років 7 місяців 8 днів і 3 роки 2 місяці 4 дні;
б) від 5 год 36 с відніміть 45 хв 40 с ;
в) 7 год 48хв 56с помножте на 18;
г) 9 тиж 21 год 52 хв розділіть на 1 тиж 23 год 44 хв.
ІІІ. Самостійне розв’язування вправ.
Тести
ІV. Підсумок. Домашнє завдання
Література
1. Н.Боровик, Л.М.Вивальнюк, М.М.Мурач,О.І.Соколенко. Курс математики. -К.:Вища школа, 1995.
2. В.М.Кухар, Б.М.Білий. Теоретичні основи початкового курсу математики.
-К. Головне видавництво видавничого об'єднання Вища школа, 1989.
3. А. М. Пышкало, Л. П. Стойлова, Н. Н. Лаврова, Н. Б.
Ирошников. Сборник задач по математике. - М.: Просвещение, 1979.
4. Л. П.Стойлова, А.М.Пышкало. Основы начального курса математики.
-М.:Просвещение, 1988.
Література
I. Курс математики: Навч. Посібник В.Н.Боровик, Л.М. Вивальнюк, М.М.Мурач, О.І.Соколенко. К.: Вища шк.,1995
II. Стойлова Л.П., Пышкало А.М. « Основы начального курса математики »: Учеб. Пособие для учащихся пед. уч-щ по спец. №2001 «Преподавание в нач. классах общеобразоват. шк.»-М.: Просвещение,1988.
III. В.М. Кухар, С.І. Тадіян, В.П.Тадіян " Математика:множини, логіка, цілі числа."- Практикум: за загал. ред. Кандидата педагогічних наук В.М. Кухар.-К.: Головне видавництво видавничого об'єднання " Вища школа", 1989.
IV. В.М. Кухар, Б.М.Білий " Теоретичні основи початкового курсу математики.": Видання друге, перероблене і доповнене.-К.: Головне вид-во видавничого об'єднання " Вища шк.", 1987.
Додатки
