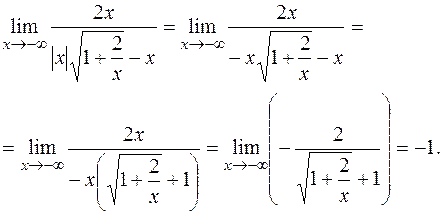Раскрытие неопределенностей

О конечных пределах

Справедливы следующие теоремы:

1. 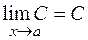, (С - постоянная)

2.

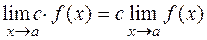
3. Если каждая из функций f(х) и g(х)имеет при 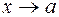конечный предел, то

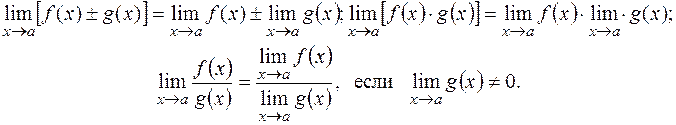Для нахождения предела элементарной функции f(х) при х→a в случае, если а - конечная точка, принадлежащая области определения f(х), нужно вычислить значение этой функции при х = а. Это значение и будет искомым пределом, т.е.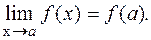

ПРИМЕР 10.Найти пределы функций при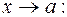

а)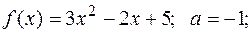

б)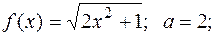

в)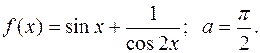

РЕШЕНИЕ:Данные функции элементарные, поэтому можно применить сформулированное правило:

а)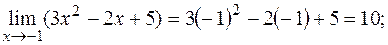

б)

в)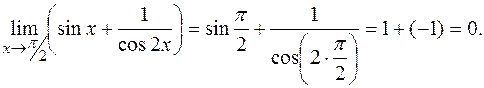

Бесконечно малые и бесконечно большие функции

Функция 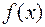называется бесконечно малой в точке а (или при 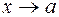), если 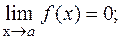функция 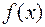называется бесконечно большой в точке а (или при 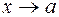), если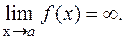

Справедливы теоремы:

1. Сумма конечного числа бесконечно малых в точке a функций -бесконечно малая функция.

2. Если f(x) - функция, ограниченная в некоторой окрестности точки а, функция g(х) - бесконечно малая в этой точке, то функция f(x) ∙ g(х) - бесконечно малая.

3. Если при 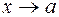функция f(x) стремится к отличному от нуля пределу, а функция g(х)- бесконечно большая при 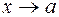, то функция f(x) ∙ g(х) - бесконечно большая при .

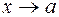4. Если функция f(x) - бесконечно малая в точке аи в некоторой окрестности этой точки не равна нулю, то функция 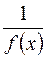- бесконечно большая в точке а; если f(x) - бесконечно большая в точке а, то 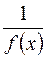- бесконечно малая.

ПРИМЕР 11.Найти a) 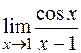; б) .

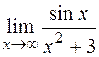РЕШЕНИЕ:

а) При 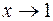функция (х - 1) - бесконечно малая, значит, 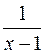- бесконечно большая, 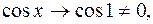следовательно, 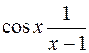- бесконечно большая, т.е.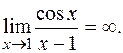

б) При 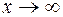функция (х² + 3) -бесконечно большая, поэтому 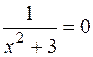- бесконечно малая. Функция sinx - ограниченная, значит, произведение 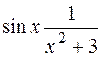- бесконечно малая, т.е.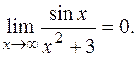

Раскрытие неопределенностей

Если при формальной подстановке предельного значения аргумента получается выражение вида

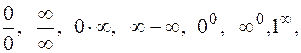
то для нахождения пределов функций необходимо проводить преобразования данных выражений.

ПРИМЕР 12.Найти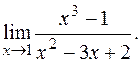

РЕШЕНИЕ:Непосредственная подстановка значения 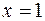приводит к неопределенности вида . Разложим на множители числитель и знаменатель дроби, выделим общий множитель и сократим на него дробь.

Для разложения числителя воспользуемся формулой:

.

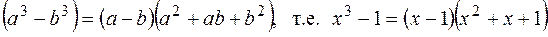В знаменателе дроби стоит квадратный трехчлен. Если квадратный трехчлен имеет корни 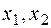, то он раскладывается на множители следующим образом: .

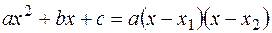Данный квадратный трехчлен имеет корни 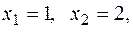поэтому 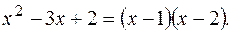Таким образом,

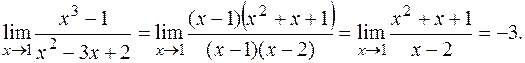
ПРИМЕР 13.Найти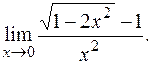

РЕШЕНИЕ: Непосредственно подставляя х = 0, получаем неопределенность . Умножим и разделим данную дробь на выражение, сопряженное числителю, то есть на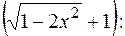

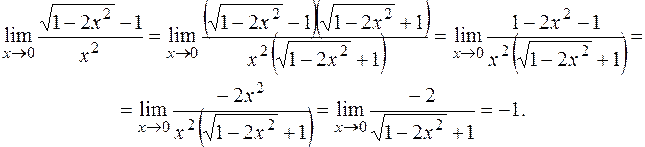
Замечание: Если в примере иррациональность имеется в числителе и знаменателе дроби, то дробь следует умножить и разделить на выражение, сопряженное числителю и на выражение, сопряженное знаменателю.

ПРИМЕР 14. Найти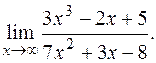

РЕШЕНИЕ: В этом примере неопределенность вида 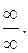Вынесем за скобки в числителе х³, а в знаменателе х² (наивысшую степень х для каждого многочлена):

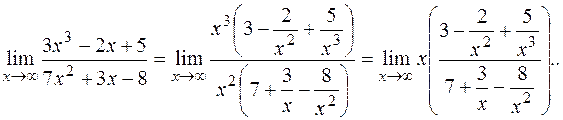
Величины 1/х, 1/х²,1/х³, обратные бесконечно большим,- бесконечно малые, и, значит, выражение в скобках стремится к 3/7. х - бесконечно большая величина, следовательно, произведение х ∙ 3/7 также величина бесконечно большая, то есть

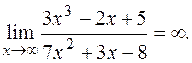
Аналогичный прием вычисления пределов можно использовать для раскрытия неопределенностей в случае иррациональных функций.

ПРИМЕР 15.Найти .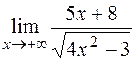

РЕШЕНИЕ:

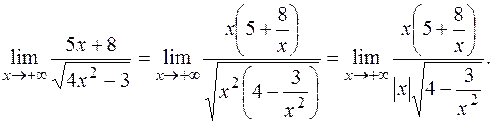
Так как 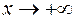, то x>0 и, значит, |x| = x. Поэтому

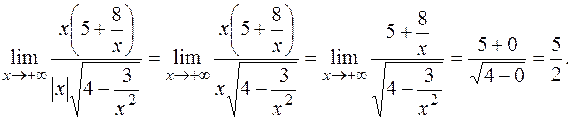
ПРИМЕР 16.Найти .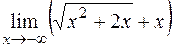

РЕШЕНИЕ:Имеем неопределенность вида ( 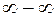). Умножим и разделим данное выражение на сопряженное:

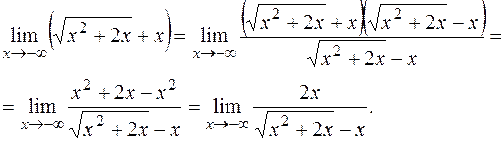
Получим неопределенность вида 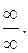Раскроем ее стандартным способом:

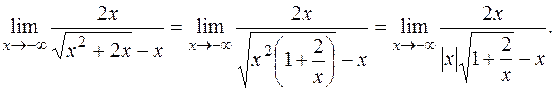
Так как 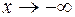, то x<0 и, значит, |x| = -x. Тогда