Основные аффинные задачи на прямые и плоскости
1. Взаимное расположение двух прямых в пространстве.
Возможны четыре случая взаимного расположения двух прямых  и
и  в пространстве: 1)
в пространстве: 1) 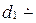
 ; 2)
; 2) 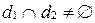 ; 3)
; 3) 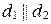 ; 4)
; 4)  совпадает с
совпадает с  .
.
Пусть прямая  задана точкой
задана точкой 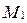 и направляющим вектором
и направляющим вектором 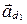 ,
,  - точкой
- точкой 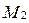 и направляющим вектором
и направляющим вектором 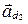 . Тогда взаимное расположение двух прямых
. Тогда взаимное расположение двух прямых  и
и  можно определить по векторам
можно определить по векторам 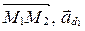 и
и 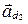 .
.
Замечание. Прямые  и
и  лежат в одной плоскости тогда и только тогда, когда векторы
лежат в одной плоскости тогда и только тогда, когда векторы 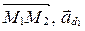 и
и 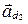 компланарны, т.е. смешанное произведение
компланарны, т.е. смешанное произведение 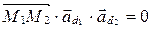 .
.
Учитывая сделанное замечание, выведем условия взаимного расположения двух прямых в пространстве.
1) 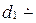
 , если не существует плоскости, содержащей одновременно обе эти прямые (рис. 75). Следовательно,
, если не существует плоскости, содержащей одновременно обе эти прямые (рис. 75). Следовательно,
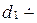
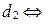
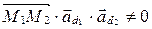 .
.
2) Если прямые  и
и  пересекаются, т.е.
пересекаются, т.е. 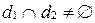 , то они лежат в одной плоскости и их направляющие векторы неколлинеарны (рис. 76). Следовательно,
, то они лежат в одной плоскости и их направляющие векторы неколлинеарны (рис. 76). Следовательно,
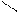
 |
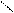 3)
3) 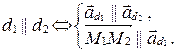 (рис. 77).
(рис. 77).
4) 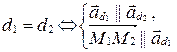 (рис. 78).
(рис. 78).
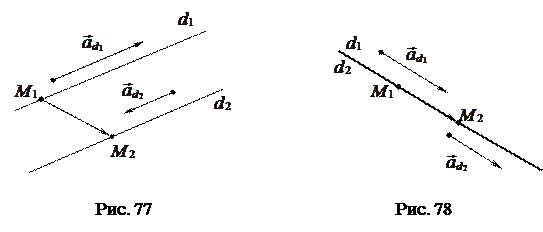 |
2. Взаимное расположение прямой и плоскости.
Возможны три случая взаимного расположения прямой 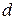 и плоскости
и плоскости 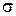 в пространстве: 1)
в пространстве: 1) 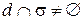 (
( 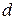 пересекает плоскость
пересекает плоскость 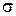 в некоторой точке); 2)
в некоторой точке); 2) 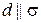 ; 3)
; 3) 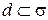 .
.
Пусть в аффинной системе координат 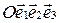 прямая
прямая 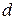 задана точкой
задана точкой 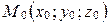 и направляющим вектором
и направляющим вектором 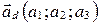 , а плоскость
, а плоскость 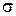 - общим уравнением
- общим уравнением 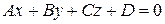 .
.
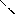 1)
1) 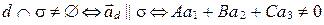 (по лемме о параллельности вектора и плоскости) (рис. 79). Итак,
(по лемме о параллельности вектора и плоскости) (рис. 79). Итак,
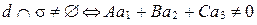 .
.
Чтобы найти координаты точки 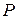 пересечения
пересечения 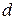 и
и 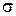 , надо решить систему уравнений прямой
, надо решить систему уравнений прямой 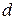 и плоскости
и плоскости 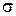 .
.
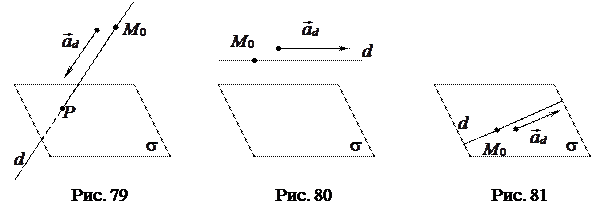 |
2) 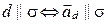 и
и 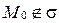 (рис. 80), т.е.
(рис. 80), т.е.
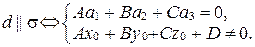
3) 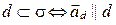 и
и 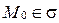 (рис. 81), т.е.
(рис. 81), т.е.
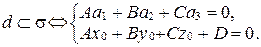
3. Связка прямых в пространстве.
Связкой прямых в пространстве с центром в точке 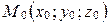 называется множество всех прямых, проходящих через точку
называется множество всех прямых, проходящих через точку 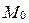 . Параметрическое уравнение связки прямых с центром
. Параметрическое уравнение связки прямых с центром 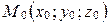 имеет вид:
имеет вид:
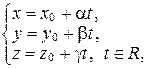
где 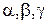 - произвольные действительные числа, не равные нулю одновременно.
- произвольные действительные числа, не равные нулю одновременно.
4. Связка прямых и плоскостей.
Объединение связки прямых в пространстве с центром 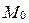 и связки плоскостей в пространстве с центром
и связки плоскостей в пространстве с центром 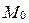 называется связкой прямых и плоскостей с центром
называется связкой прямых и плоскостей с центром 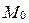 .
.
Каждые две (различные) плоскости связки пересекаются по прямой связки, и каждая прямая связки является осью пучка плоскостей связки. Следовательно, множество прямых, по которым пересекаются плоскости связки, есть связка прямых с центром 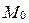 .
.
Задания для самостоятельной работы
1. Запишите в координатном виде условие того, что прямые 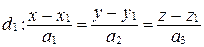 и
и 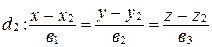 являются скрещивающимися.
являются скрещивающимися.
2. Запишите в координатном виде условие того, что прямые  и
и  (см. задание 1) пересекаются.
(см. задание 1) пересекаются.
3. Запишите в координатном виде условие параллельности прямых  и
и  (см. задание 1).
(см. задание 1).
4. Запишите в координатном виде условие совпадения прямых  и
и  (см. задание 1).
(см. задание 1).
5. Выясните взаимное расположение прямой 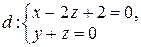 и оси: а)
и оси: а) 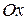 ; б)
; б) 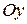 ; в)
; в) 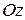 аффинной системы координат
аффинной системы координат 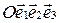 .
.
6. Выясните взаимное расположение прямой 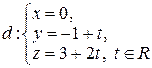 и координатной плоскости: а)
и координатной плоскости: а) 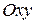 ; б)
; б) 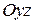 ; в)
; в) 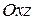 .
.
Основные метрические задачи
