Разбиение на элементарные звенья

Запишем передаточную функцию разомкнутой системы:

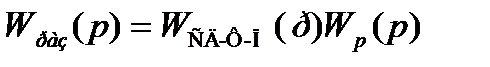
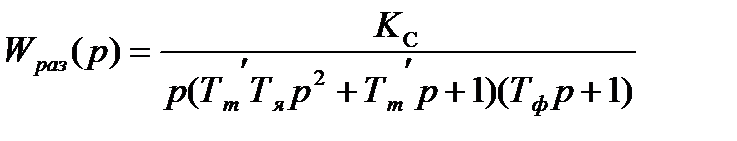
(7.1)

Разобьем на элементарные звенья:

1)

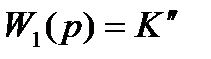
Где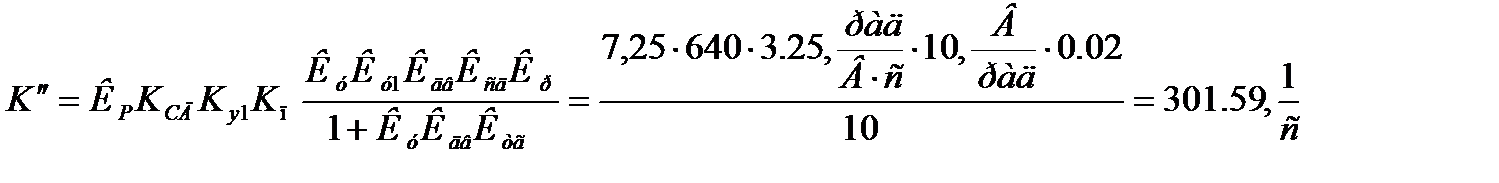

Это пропорциональное звено.

2)

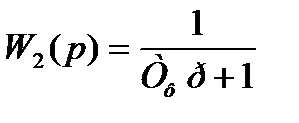
Это апериодическое звено. Т_ф=0.006 с

ω_ф=1/Т_ф=1/0.006=166.667 рад/с

lg(ω_ф)=2.2218

3)

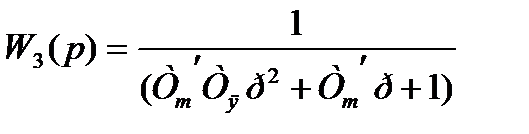
Данное звено является колебательным так как уравнение 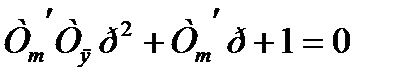не имеет действительных корней относительно p.

Приведем к нормальному виду колебательного звена:

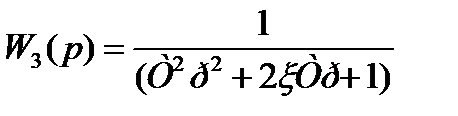
(7.2)

Где ,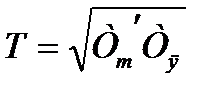

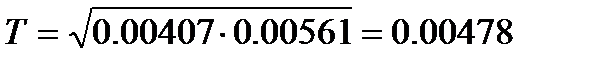
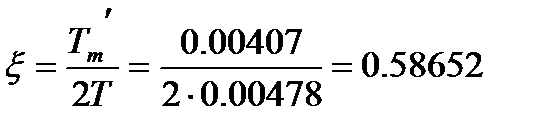
4)

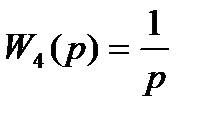
Интегрирующее звено ЛАЧХ – наклонная прямая, -20 дБ/дек.

ЛФЧХ параллельна оси частот и проходит на уровне .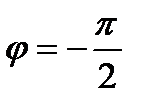

7.2 Построение желаемой ЛАХ.

Начинается с построения среднечастотной ЛАХ. По заданным параметрам: времени регулирования t_p(с) и динамической ошибке s% определяем по номограмме (рис7.1) ω_ср: примем s = 23%

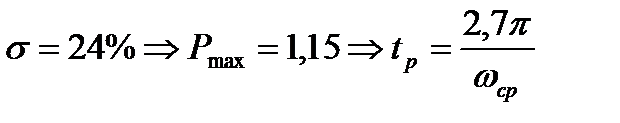
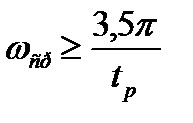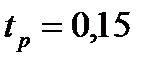Из приведённой формулы следует .При с, 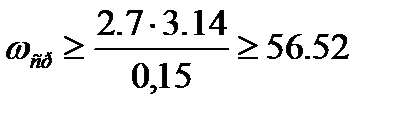, 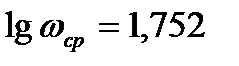дБ/дек

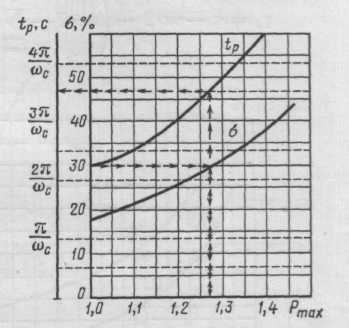
Рис 7.1.

Для указанного выбора по раннее найденному значению Р_max с помощью кривых (рис7.2) определим избыток фазы γ и предельные значения L_M логарифмических амплитуд. Избыток фазы γ должен быть обеспеченна том участке характеристики L_ж(ω), для которого справедливо

L_M ≥ L_ж(ω) ≥ - L_M

Этот участок охватывает среднечастотную асимптоту и, возможно, часть сопрягающей асимптоты.

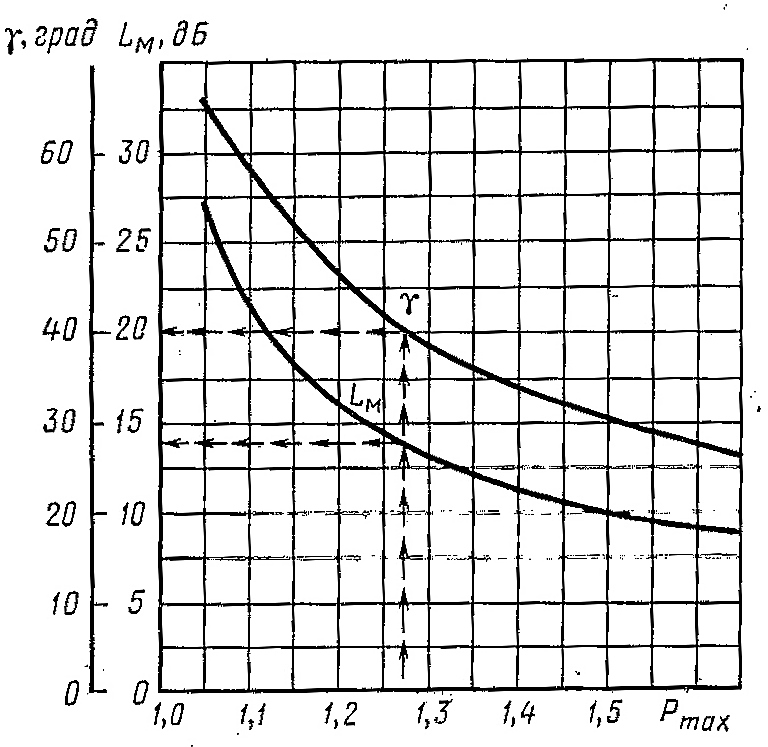
Рис.7.2.

Сначала проведём прямую с ординатой L_M.Затем наносим сопрягающую асимптоту.

Проверка избытка фазы γ₂. По приблизительной формуле:

избыток фазы больше необходимого γ=40^о (который определяется с помощью кривых рисунок 7.2). Сопряжение среднечастотной желаемой ЛАХ с низкочастотной частью исходной ЛАХ проводится под наклоном -40дб/дек до пересечения при ω₁.с ЛАХ L₀(ω).

Высокочастотная асимптота желаемой ЛАЧХ мало влияет на свойства системы. Поэтому выберем её, так чтобы корректирующее устройство было возможно более простым.

Построение с высокочастотной части ЛАХ проводится под наклоном при ω₃ -40дб/дек и при ω₄.-80дб/дек параллельно исходным асимптотам ЛАХ L₀(ω). Передаточная функция желаемой разомкнутой системы определится по ЛАХ.

Проверка избытка фазы γ_ф при ω_ф:

избыток фазы больше необходимого γ=40^о. Следовательно желаемая ЛАЧХ построена правильно. Запишем передаточную функцию:

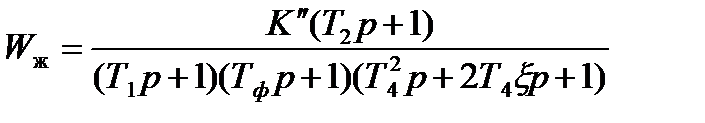
(7.5)

7.3Выбор корректирующих устройств.

Передаточная функция W_ж(p)=W₀(p)W_к(p), от куда следует

L_к(ω)=L_ж(ω) - L₀(ω)

Это изображено на ЛАХ

Передаточная функция корректирующей системы:

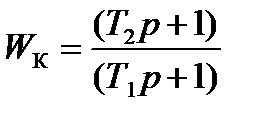(7.6)

ω₁=10^0.5=3.16; Т₁=1/ω₁=0.316 с,

ω₂=10^1.1=12.6; Т₂=1/ω₂=0.0794 с.

Для второго корректирующего звена 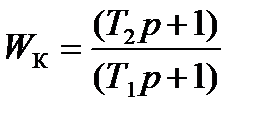подбираем интегрирующее пассивное корректирующее звено:

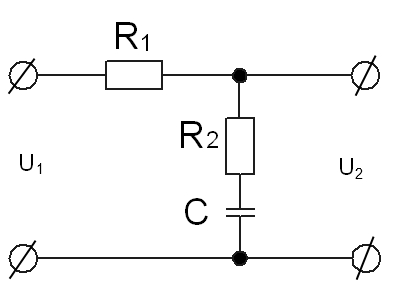
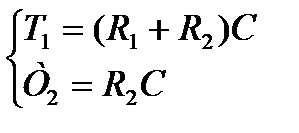(7.7)

Зададимся емкостью конденсатора равной 1 мкФ. Отталкиваясь от емкости конденсатора, найдем сопротивления резисторов.
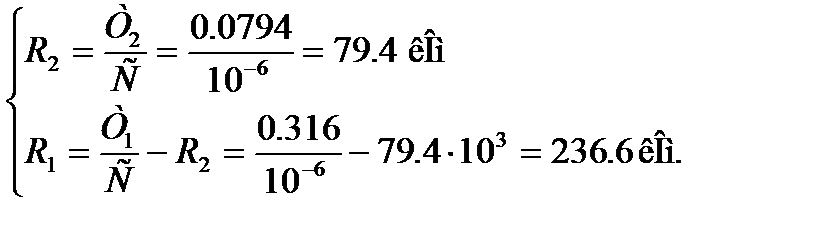
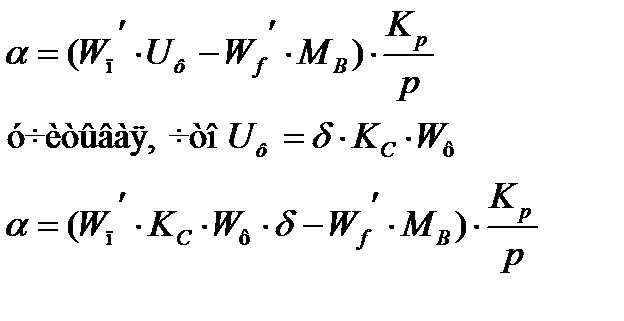