Способы задания функции
Существует несколько способов задания функции.
Табличный. Используется тогда, когда область определения состоит из
конечного множества чисел. Тогда для задания функции проще всего указать
таблицу, содержащую значения аргумента и соответствующие значения
функции. Например, таблица логарифмов. Другим примером могут быть
таблицы, содержащие данные о числе жителей, населяющих земной шар в
отдельные годы, расписания движения поездов и т.п.
Аналитический. При аналитическом способе задания функция может
быть задана явно, когда дано выражение у через x, т.е. формула имеет вид
y f (x) ; неявно, когда х и у связаны между собой уравнением вида F(x, y) 0 ;
параметрически, когда соответствующие друг другу значения х и у выражены
через третью переменную величину t, называемую параметром.
Логический. Если функция описывается правилом ее составления,
например, функция Дирихле: f(x)= 1, если x – рациональное; f(x)= 0, если x –
иррациональное.
Графический. Состоит в изображении графика функции – множества
точек (x, y) плоскости, абсциссы которых есть значения аргумента x, а
ординаты – соответствующие им значения функции y f (x) . Преимуществом
графического задания является его наглядность, недостатком – его
неточность.
32.
Определение элементарной функции.
Функции, которые могут быть получены из основных элементарных функций посредством арифметических действий (сложение, вычитание, умножение, деление) и образования сложных функций, называютсяэлементарными функциями.
Примером может являться функция 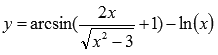
Очень удобно классификацию элементарных функций представить в виде таблицы.
- Элементарные функции
- Трансцендентные
- Алгебраические
- Иррациональные
- Рациональные
- Целые рациональные
- Дробные рациональные
Элементарные функции подразделяются на алгебраические и трансцендентные.
Определениеалгебраических функций.
Алгебраическими называют функции, составленные из букв и цифр, соединенных знаками действий сложение, умножение, вычитание, деление, возведение в целую степень и извлечение корня.
Другими словами: алгебраическими называют элементарные функции, которые могут быть получены из двух основных функций f(x)=x и f(x)=1 при помощи любого числа последовательно выполненных алгебраических действий (сложение, умножение, вычитание, деление, возведение в целую степень, извлечение корня) и умножения на числовые коэффициенты.
Например, функция 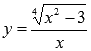 является алгебраической.
является алгебраической.
Определение трансцендентной функции.
Трансцендентными называют элементарные функции, которые не являются алгебраическими. (То есть, они образованы при помощи возведения в иррациональную степень, логарифмирования, с использованием тригонометрических и обратных тригонометрических операций).
К примеру, 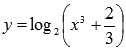 - трансцендентная функция.
- трансцендентная функция.
Алгебраические функции подразделяются на рациональные и иррациональные .
Рациональные функции разделяются на целые рациональные функции (многочлены) и дробные рациональные (отношение многочленов).
Пример целой рациональной функции: 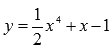 .
.
Пример дробно-рациональной функции: 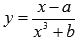 .
.
ПРИМЕЧАНИЕ:
Рациональные функции могут содержать и иррациональные коэффициенты (главное, чтобы под знаком радикала не было аргумента функции). Например, 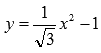 - целая рациональная функция, а не иррациональная.
- целая рациональная функция, а не иррациональная.
Определение иррациональной функции.
Иррациональными называются алгебраические функции, содержащие аргумент под знаком радикала (корня).
Примером может являться функция 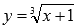 .
.
ПРИМЕЧАНИЕ:
Если вид функции можно упростить на всей области определения, то классификации подлежит именно упрощенная функция.
К примеру, 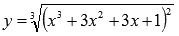 - не иррациональная функция, а рациональная, так как
- не иррациональная функция, а рациональная, так как 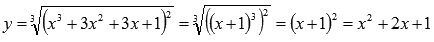 ;
;
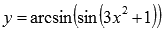 - не трансцендентная функция, а рациональная алгебраическая, так как
- не трансцендентная функция, а рациональная алгебраическая, так как 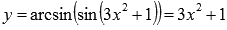 .
.
| Понятие о сложной функции Пусть даны две функции z = f(y) и у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)) (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точке у). |
Пример. Функцию 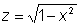 можно рассматривать как композицию функций можно рассматривать как композицию функций 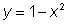 и и 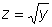 . . |
Для записи композиции функций употребляется значок 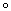 . Например, запись . Например, запись 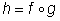 означает, что функция h получена как композиция функций f и g (сначала применяется g, а затем f), т. е. означает, что функция h получена как композиция функций f и g (сначала применяется g, а затем f), т. е. 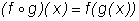 . Операция образования сложной функции (или композиция функций) не обладает переместительным свойством: . Операция образования сложной функции (или композиция функций) не обладает переместительным свойством: 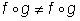 . Чтобы можно было вычислить сложную функцию h = f(g(x)), надо, чтобы число g(x), т. е. значение функции g, попадало в область определения функции f . . Чтобы можно было вычислить сложную функцию h = f(g(x)), надо, чтобы число g(x), т. е. значение функции g, попадало в область определения функции f . |
Пример. 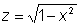 Вычисляя значения функции Вычисляя значения функции 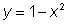 , необходимо брать только те числа х, для которых , необходимо брать только те числа х, для которых 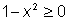 , т. е. те, для которых число , т. е. те, для которых число 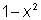 попадает в область определения функции попадает в область определения функции 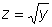 . . |
| 2. Взаимно обратные функции Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную у. Выразив х через у, мы получим равенство вида х = g(y). В этой записи g обозначает функцию, обратную к f. Если функция g является обратной для функции f, то и функция является обратной для функции g. Пару функций f и g называют взаимно обратными функциями. |
33.
Последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров x1,x2,...xn
Числа x1,x2,...,xn — называются элементами последовательности, символ xn — общим элементом, а число n — его номером. Сокращенно последовательность обозначается символом {xn}.
Счетным множеством называется множество эквивалентное множеству натуральных чисел. Следовательно любая последовательность является счетным множеством.
