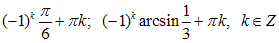При решении уравнений необходимо знать основные тригонометрические формулы

Примеры и последовательность выполнения заданий по преобразованию степенных выражений

Пример 1. Вычислить

а)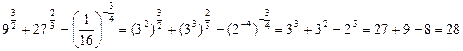

б)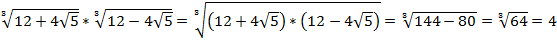

в)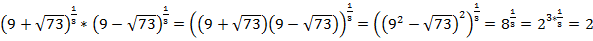

г)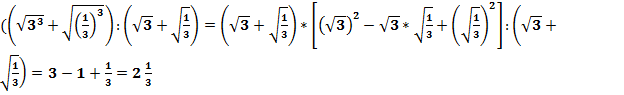

д)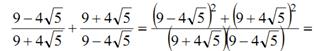

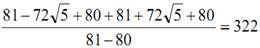
Пример 2. Упростить выражение и найти его значение

а) 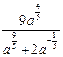при а = 5

Решение

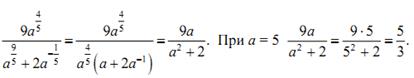
б) 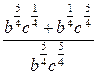при b=2, c=5

Решение

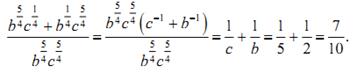
Пример 3. Избавиться от иррациональности в знаменателе

а) 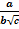Решение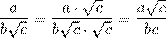

б) 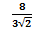Решение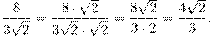

в) 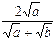Решение .

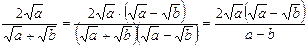г) 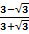Решение: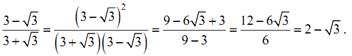

д) 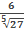Решение:

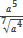Решение :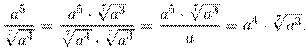

ЛОГАРИФМЫ. ПРИМЕРЫ С РЕШЕНИЯМИ

1. Вычислите .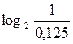

Решение. 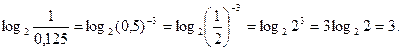Ответ: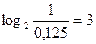

2. Вычислите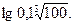

Решение.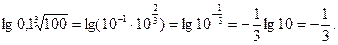

3. Вычислите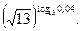

Решение.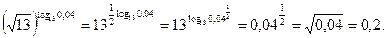

4. Вычислите .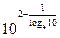

Решение. Т. к. выражение 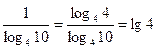, то решение принимает вид:

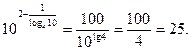
5. Найдите значение выражения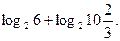

Решение.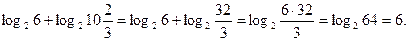

6. Найдите значение выражения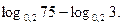

Решение.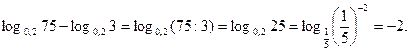

7. Вычислите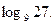

Решение.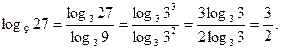

8. Известно, что 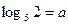. Найдите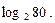

Решение.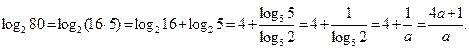

9. Найдите значение выражения .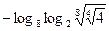

Решение.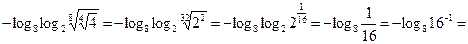

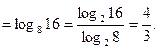
10. Найдите 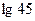, если .

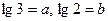Решение.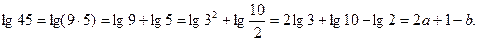

11. Вычислить: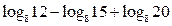

На основе формул преобразуем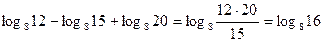

Теперь можно перейти к новому основанию, в данном примере логарифмы чисел 16 и 8 легко вычислить при основании 2, тогда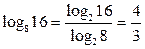

12.Вычислить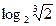

Применим формулу (5), для этого вспомним определение степени с рациональным показателем ( 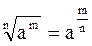), тогда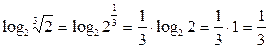

13.Зная, что 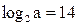, найти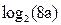

Применяем формулу (3)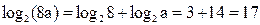

14.

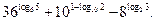
Решение:

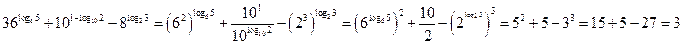15.

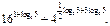
Решение:

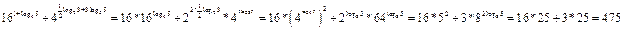
16. .

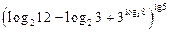Решение:

=

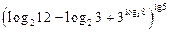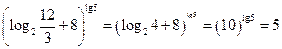
17.Вычислите

.

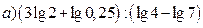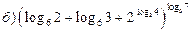
Решение:

=

=

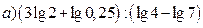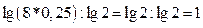
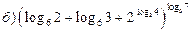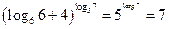
Решение логарифмических уравнений

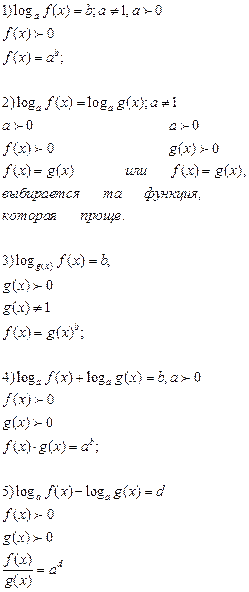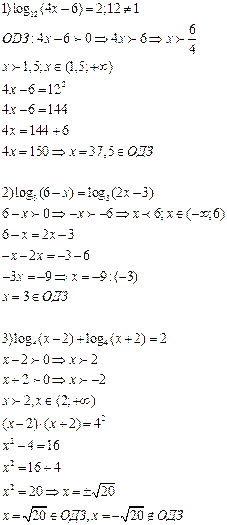Примеры и последовательность выполнения заданий.

1. Простейшее логарифмическое уравнение:

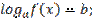
ОДЗ: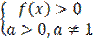

Решение:

1) ;

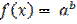2) Отбор корней, удовлетворяющих ОДЗ.

Пример:

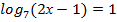
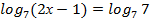
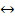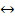2х-1=7 2х=8 х=4

Проверка: 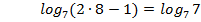=1

1=1

Ответ: х=4.

По свойству логарифмов и определение логарифма

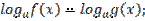
ОДЗ: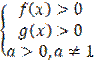

1)Решить f(x)=g(x)

2)Отбор корней, удовлетворяющих ОДЗ.

Пример:

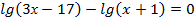
ОДЗ:

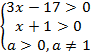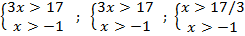; x .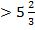

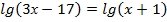
3x-17=x+1

3x-x=17+1

2x=18

x=9 - уд. ОДЗ

Ответ: х=9

Замечание: Можно решить без ОДЗ, но тогда обязательна проверка!

3.Если в уравнении логарифмы с разными основаниями

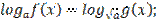
ОДЗ: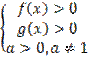

1)Сведите логарифмы к одному основанию

2)Отбор корней, удовлетворяющих ОДЗ.

Пример 1:

,

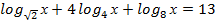
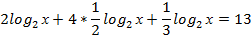
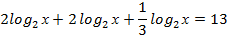
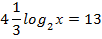
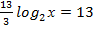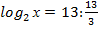
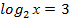, х=2³ , х=8

Ответ: х=8.

ТРИГОНОМЕТРИЯ

Например: а) Выразить в радианной мере углы 40⁰, 320⁰;

б) Выразить в градусной мере углы .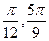

Решение:

а) ;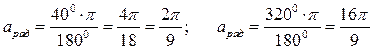

б) .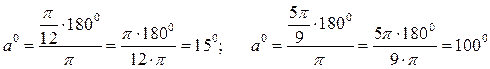

2. Задание – найти все тригонометрические функции:

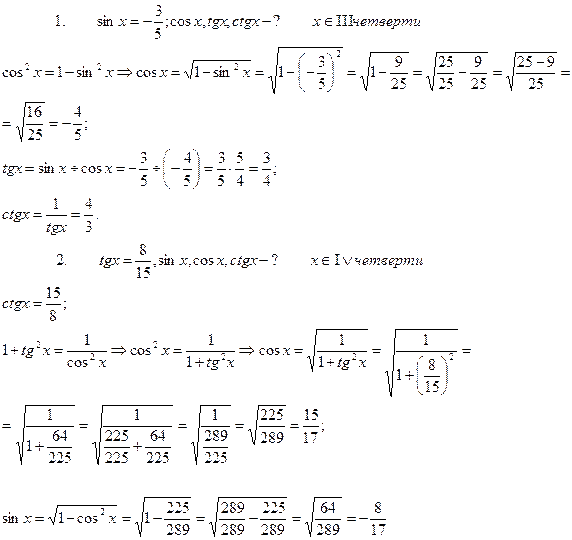
Замечание:

при решении подобных упражнений необходимо учитывать четверть, в которой находится угол, т.к. от этого зависит знак определяемого значения функции.

Тригонометрические уравнения.

Пример 1: Решить уравнение .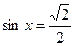

Ответ: По формуле получаем

х = (-1)^п arcsin 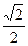+ πп, п 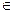Z;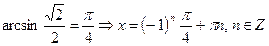

Пример 2: Решить уравнения: .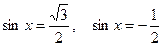

Ответ: По формуле получаем 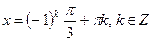и .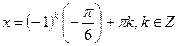

Пример 3: Решить уравнения: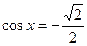

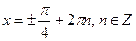
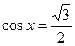
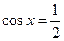
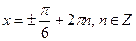
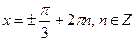
Пример 4: Решить уравнения: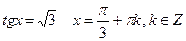

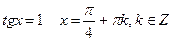
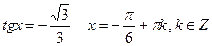
Пример 5: Решить уравнения: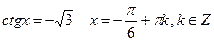

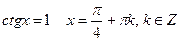
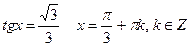
Пример 6: Решить уравнение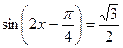

Ответ: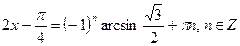

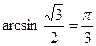
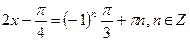
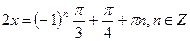
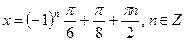
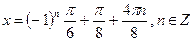
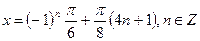
Пример 7: Решить уравнение вида .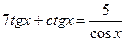

Ответ: Приведем к виду .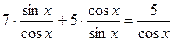

Найдем общий знаменатель и преобразуем

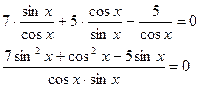
Так как 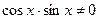, то

.

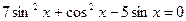Используем основное тригонометрическое тождество 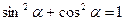, получим

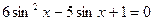, делаем замену

sin x = t и решаем полученное квадратное уравнение.

Получаем следующие значения:

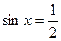и .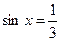

Решив эту уравнения, найдем

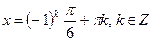и .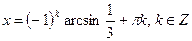

При решении уравнений необходимо знать основные тригонометрические формулы.

Пример 1. Решить уравнение .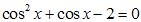

Решение. Это уравнение является квадратным относительно 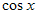. Поэтому сделаем замену 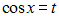. В результате получим уравнение 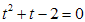. Его корни: 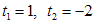, то есть получаем уравнение 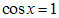или 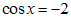. Первое уравнение дает 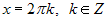. Второе уравнение не имеет корней.

Ответ: .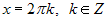

Пример 2. Решить уравнение .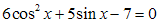

Решение. Так как 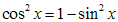, то уравнение можно представить в виде ;

.

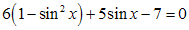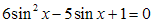Сделаем замену 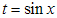. Получим квадратное уравнение 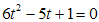, решая которое, имеем: 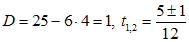, то есть .

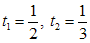Таким образом, получим два простейших уравнения 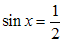или .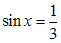

Решая их, имеем 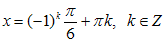или .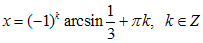

Ответ: