Тема: «Элементы аналитической геометрии на плоскости и в пространстве»

1. Дано уравнение прямой в плоскости A x + B y + C = 0. Данное уравнение – это уравнение:

+: в общем виде;

-: каноническое;

-: параметрическое;

-: через две заданные точки;

-: в отрезках;

-: через заданную точку и нормальный вектор.

2. Дано уравнение прямой в плоскости 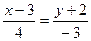. Данное уравнение – это уравнение:

-: в общем виде;

+: каноническое;

-: параметрическое;

-: через две заданные точки;

-: в отрезках;

-: через заданную точку и нормальный вектор.

3. Дано уравнение прямой в плоскости 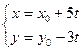. Данное уравнение – это уравнение:

-: в общем виде;

-: каноническое;

+: параметрическое;

-: через две заданные точки;

-: в отрезках;

-: через заданную точку и нормальный вектор.

4. Дано уравнение прямой на плоскости 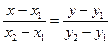. Данное уравнение – это уравнение:

-: в общем виде;

-: каноническое;

-: параметрическое;

+: через две заданные точки;

-: в отрезках;

-: через заданную точку и нормальный вектор.

5. Дано уравнение прямой на плоскости 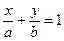. Данное уравнение – это уравнение:

-: в общем виде;

-: каноническое;

-: параметрическое;

-: через две заданные точки;

+: в отрезках;

-: через заданную точку и нормальный вектор.

6. Дано уравнение прямой на плоскости A (x – x₁) + B (y – y₁) + C = 0. Данное уравнение – это уравнение:

-: в общем виде;

-: каноническое;

-: параметрическое;

-: через две заданные точки;

-: в отрезках;

+: через заданную точку и нормальный вектор.

7. Уравнение прямой на плоскости через точку М(3; -2) и направляющий вектор а = (-5; 3) имеет вид:

-: ;

+: ;

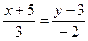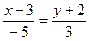+: 3 х + 5 у + 1 =0;

-: 2 х + 10 у + 19 =0

8. Уравнение прямой на плоскости через точку М(1; -4) и направляющий вектор а = (6; 2) имеет вид:

-: ;

+: ;

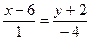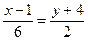+: х - 3 у - 13 =0;

-: 4 х + у - 22 =0.

9. Уравнение прямой на плоскости 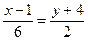имеет направляющий вектор:

+: а = (6; 2);

-: а = (-1; 4);

-: а = (1; -4);

-: а = (-6; -2).

10. Уравнение прямой на плоскости 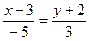имеет направляющий вектор:

+: а = (-5; 3);

-: а = (-3; 2);

-: а = (5; -3);

-: а = (3; -2).

11. Нормальный вектор к прямой х - 3 у - 13 =0 имеет координаты:

+: N = (1; -3)

-: N = (-3; -13)

-: N = (1; -13)

-: N = (1; -16)

12. Уравнение прямой на плоскости 3 х + 5 у + 1 =0 имеет нормальный вектор:

+: N = (3; 5);

-: N = (8; 1);

-: N = (3; 5; 1);

-: N = (5; 3).

13. Уравнение прямой на плоскости, проходящей через точку М₁(2; 3) и точку М₂(7; 5) имеет вид:

-: ;

+: ;

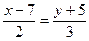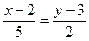+: 2х - 5 у + 11 =0;

-: 3 х - 2у - 31 =0.

14. Уравнение прямой на плоскости, проходящей через точку М₁(1; 3) и точку М₂(4; 1) имеет вид:

-: ;

+: ;

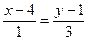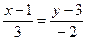+: 2х - 3 у - 11 =0;

-: 3 х - у - 11 =0.

15. Уравнение прямой на плоскости 2х - 3 у - 11 =0 имеет нормальный вектор:

+: N = (2; -3);

-: N = (2; -3; -11);

-: N = (-3; 2);

-: N = (-1; -11).

16. Уравнение прямой на плоскости 2х - 5 у + 11 =0 имеет нормальный вектор:

+: N = (2; -5);

-: N = (2; -5; 11);

-: N = (-3; 11);

-: N = (5; -11).

17. Уравнение прямой, проходящей через заданную точку М(5; 3) и имеющую нормальный вектор N = (5; -4) имеет вид:

+: 5 х – 4 у -13 = 0;

-: 5 х + 3 у -13 = 0;

-: 5 х – 4 у + 8 = 0;

-: 10 х – у + 8 = 0.

18. Уравнение прямой на плоскости 5 х – 4 у -13 = 0 имеет нормальный вектор:

+: N = (5; -4);

-: N = (5; -4; -13);

-: N = (-13; -4; 5);

-: N = (1; -13).

19. Уравнение прямой, проходящей через заданную точку М(-7; 2) и имеющую нормальный вектор N = (4; 3) имеет вид:

+: 4 х + 3 у +22 = 0;

-: -7 х + 2 у + 22 = 0;

-: -3 х + 5 у + 22 = 0;

-: 7 х – 2у - 22 = 0.

20. Уравнение прямой на плоскости 4 х + 3 у +22 = 0 имеет нормальный вектор:

+: N = (4; 3);

-: N = (4; 3; 22);

-: N = (22; 3; 4);

-: N = (7; 22).

21. Среди пар прямых указать параллельные:

-: 2 х – 3 у + 5 =0 и 14 х + 21 у -13 =0;

+: 2 х – 3 у + 5 =0 и 6 х - 9 у +1 =0;

-: 6 х – 3 у - 1 =0 и 2 х - 5 у + 5 =0;

+: 6 х + 10 у + 1 =0 и 3 х + 5 у =0.

22. Среди пар прямых указать перпендикулярные:

+: 3 х – 2 у + 17 =0 и 2 х + 3 у -16 =0;

-: 2 х – 3 у + 5 =0 и 6 х - 9 у +1 =0;

+: 6 х – 4 у - 9 =0 и 2 х + 3 у - 16 =0;

+: 2 х - 7 у + 5 =0 и 21 х + 6 у – 2 =0.

23. Даны уравнения двух прямых 4х + 6у - 9 = 0 и 3х + 2у + 12 = 0. Эти прямые

-: параллельны;

-: перпендикулярны;

+: пересекаются под острым углом;

-: ничего нельзя сказать

24. Угол между прямыми у = 2х – 3 и 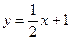равен:

-: ;

+: ;

-: ;

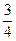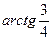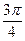-: 135⁰.

25. Угол между прямыми 5х – у + 7 = 0 и 2х – 3у + 1 = 0 равен:

+: 45⁰;

+: ;

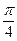-: 60⁰;

-: .

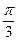26. Координаты точки пересечения прямых 3х – 2у + 1 = 0 и 2х + 5у - 12 = 0:

-: (2; 1);

+: (1; 2);

-: (1; -12);

-: (8; -11).

27. Расстояние от точки М(2; 1) до прямой 3х + 4у - 90 = 0 равно:

-: 3;

-: 4;

-: 14;

+: 16.

28. Расстояние от точки М(3; 2) до прямой 5х + 12у + 39 = 0 равно:

-: 75

-: 5;

-: 41;

+: 6.

29. Уравнение прямой на плоскости через точку М(2; -3) и направляющий вектор а = (3; 6) имеет вид:

-: ;

+: ;

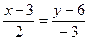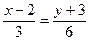+: 2х - у - 7 =0;

-: 3 х + 2у - 21 =0.

30. Уравнение прямой на плоскости, проходящей через точку М₁(3; -1) и точку М₂(2; 4) имеет вид:

-: ;

+: ;

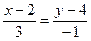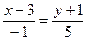+: 5х + у - 14 =0;

-: х + 3у - 14 =0.

31. Уравнение прямой, проходящей через заданную точку М(4; -5) и имеющую нормальный вектор N = (2; -3) имеет вид:

+: 2 х – 3 у -23 = 0;

-: 4 х - 5 у -13 = 0;

-: 6 х – 8 у + 8 = 0;

-: 2 х – 3у - 1 = 0.

32. Уравнение плоскости, проходящей через точку М(5; 5; 0) и имеющей нормальный вектор N = (4; 3; 2) имеет вид:

-: 5х + 5у - 35 = 0;

+: 4х + 3у + 2 z - 35 = 0;

-: 9х + 8у + 2 z - 35 = 0;

-: х + 2у - 2 z - 35 = 0.

33. Уравнение плоскости, проходящей через точку М(1; 2; 3) и имеющей нормальный вектор N = (1; 2; 3) имеет вид:

-: 3х + 2у + z - 14 = 0;

-: 2х + 4у + 6 z - 12 = 0;

-: х + 2у + 3 z - 6 = 0;

+: х + 2у + 3 z - 14 = 0.

34. Уравнение плоскости, параллельной оси ОX и проходящей через точки М₁(0; 1; 3) и М₂(2; 4; 5), имеет вид:

-: у + 3z - 11 = 0;

-: 2х + 5у + 8 z + 7 = 0;

-: 2х + 4у + 5 z - 4 = 0;

+: 2у - 3 z + 7 = 0.

35. Уравнение плоскости, параллельной оси ОZ и проходящей через точки М₁(3; 1; 0) и М₂(1; 3; 0), имеет вид:

-: 4x + 4у - 11 = 0;

+: х + у - 4 = 0;

-: х + 3у - 4 = 0;

-: x + у - 3 z = 0.

36. Двугранный угол между плоскостями 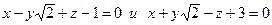равен:

+: ;

+: ;

-: ;

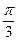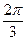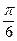-: 30⁰.

37. Двугранный угол между плоскостями у - 3 z = 0 и 2у + z = 0 равен:

+: ;

+: ;

-: ;

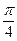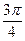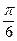-: 30⁰.

38. Уравнение плоскости, проходящей через точки М₁(3; 3; -1), М₂(0; 2; 5), М₃(1; 1; 1), имеет вид:

+: 5x - 3у + 2z - 4 = 0;

-: 3x - 5у + 4z - 2 = 0;

-: 6x - 4у + z - 3 = 0;

-: 2x + у + 4z - 5 = 0.

39. Уравнение плоскости, проходящей через точки М₁(1; 2; 3), М₂(2; 0; -7), М₃(1; 1; 1), имеет вид:

+: 6x - 2у + z - 5 = 0;

-: 2x + у - z + 1 = 0;

-: 5x + 4у + z - 3 = 0;

-: 6x - 4у + 5z + 3 = 0.

40. Расстояние от точки М(5; 1; -1) до плоскости х - 2у – 2 z + 4 = 0 равно:

+: 3;

-: 4;

-: 9;

-: 17,6.

41. Расстояние от точки М(1; 3; -2) до плоскости 2х - 3у – 4 z + 28 = 0 равно:

-: 3;

-: 4;

+: ;

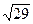-: 17,6.

42. Уравнение плоскости, проходящей через начало координат перпендикулярно к двум плоскостям 2x - у + 3z - 1 = 0 и x + 2у + z = 0, имеет вид:

-: 7x - у - 5z + 1 = 0;

+: 7x - у - 5z = 0;

-: 3x + у + 4z - 1 = 0;

-: x - 3у + 2z - 1 = 0.

43.Уравнение прямой, проходящей через заданную точку М(4; 3; 2) и имеющей направляющий вектор а = (-1; 1; 1), имеет вид:

+:

-:

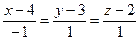
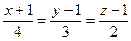
+: 3 x = 4 y – 7 x = 2 z - 3

-: x – y – z + 1 = 0

44. Координаты вектора, параллельного прямой :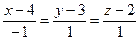

-: а = (4; 3; 2)

+: а = (-1; 1; 1)

+: а = (1; -1; -1)

-: а = (-4; -3; -2)

45. Координаты точки, принадлежащей прямой :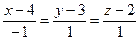

+: М(4; 3; 2)

-: М (-1; 1; 1)

-: М(1; -1; -1)

-: М (-4; -3; -2)

46. Какие точки принадлежат прямой :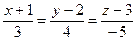

-: М(3; 4; -5);

-: М (1; -2; -3)

+: М(-1; 2; 3)

+: М (2; 6; -2)

47. Определить прямую, параллельную прямой :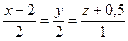

+:

-:

-:

-:

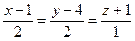
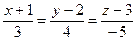
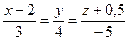
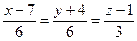
48. Дано уравнение прямой в плоскости A x + B y + C = 0. Данное уравнение – это уравнение:

+: в общем виде;

-: каноническое;

-: параметрическое;

-: через две заданные точки;

-: в отрезках;

-: через заданную точку и нормальный вектор.

49. Дано уравнение прямой в плоскости 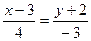. Данное уравнение – это уравнение:

-: в общем виде;

+: каноническое;

-: параметрическое;

-: через две заданные точки;

-: в отрезках;

-: через заданную точку и нормальный вектор.

50. Дано уравнение прямой в плоскости 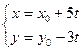. Данное уравнение – это уравнение:

-: в общем виде;

-: каноническое;

+: параметрическое;

-: через две заданные точки;

-: в отрезках;

-: через заданную точку и нормальный вектор.

51.Дано уравнение прямой на плоскости 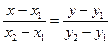. Данное уравнение – это уравнение:

-: в общем виде;

-: каноническое;

-: параметрическое;

+: через две заданные точки;

-: в отрезках;

-: через заданную точку и нормальный вектор.

52. Дано уравнение прямой на плоскости 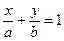. Данное уравнение – это уравнение:

-: в общем виде;

-: каноническое;

-: параметрическое;

-: через две заданные точки;

+: в отрезках;

-: через заданную точку и нормальный вектор.

53. Дано уравнение прямой на плоскости A (x – x₁) + B (y – y₁) + C = 0. Данное уравнение – это уравнение:

-: в общем виде;

-: каноническое;

-: параметрическое;

-: через две заданные точки;

-: в отрезках;

+: через заданную точку и нормальный вектор.

54. Уравнение прямой на плоскости через точку М(3; -2) и направляющий вектор а = (-5; 3) имеет вид:

-: ;

+: ;

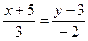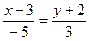+: 3 х + 5 у + 1 =0;

-: 2 х + 10 у + 19 =0

55. Уравнение прямой на плоскости через точку М(1; -4) и направляющий вектор а = (6; 2) имеет вид:

-: ;

+: ;

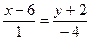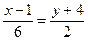+: х - 3 у - 13 =0;

-: 4 х + у - 22 =0.

56. Уравнение прямой на плоскости 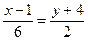имеет направляющий вектор:

+: а = (6; 2);

-: а = (-1; 4);

-: а = (1; -4);

-: а = (-6; -2).

57. Уравнение прямой на плоскости 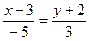имеет направляющий вектор:

+: а = (-5; 3);

-: а = (-3; 2);

-: а = (5; -3);

-: а = (3; -2).

58. Нормальный вектор к прямой х - 3 у - 13 =0 имеет координаты:

+: N = (1; -3)

-: N = (-3; -13)

-: N = (1; -13)

-: N = (1; -16)

59. Уравнение прямой на плоскости, проходящей через точку М₁(2; 3) и точку М₂(7; 5) имеет вид:

-: ;

+: ;

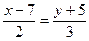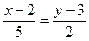+: 2х - 5 у + 11 =0;

-: 3 х - 2у - 31 =0.

60. Уравнение прямой на плоскости, проходящей через точку М₁(1; 3) и точку М₂(4; 1) имеет вид:

-: ;

+: ;

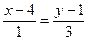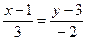+: 2х - 3 у - 11 =0;

-: 3 х - у - 11 =0.

61. Среди пар прямых указать параллельные:

-: 2 х – 3 у + 5 =0 и 14 х + 21 у -13 =0;

+: 2 х – 3 у + 5 =0 и 6 х - 9 у +1 =0;

-: 6 х – 3 у - 1 =0 и 2 х - 5 у + 5 =0;

+: 6 х + 10 у + 1 =0 и 3 х + 5 у =0.

62.Среди пар прямых указать перпендикулярные:

+: 3 х – 2 у + 17 =0 и 2 х + 3 у -16 =0;

-: 2 х – 3 у + 5 =0 и 6 х - 9 у +1 =0;

+: 6 х – 4 у - 9 =0 и 2 х + 3 у - 16 =0;

+: 2 х - 7 у + 5 =0 и 21 х + 6 у – 2 =0.

63. Даны уравнения двух прямых 4х + 6у - 9 = 0 и 3х + 2у + 12 = 0. Эти прямые

-: параллельны;

-: перпендикулярны;

+: пересекаются под острым углом;

-: ничего нельзя сказать

64. Расстояние от точки М(2; 1) до прямой 3х + 4у - 90 = 0 равно:

-: 3;

-: 4;

-: 14;

+: 16.

65. Уравнение плоскости, параллельной оси ОX и проходящей через точки М₁(0; 1; 3) и М₂(2; 4; 5), имеет вид:

-: у + 3z - 11 = 0;

-: 2х + 5у + 8 z + 7 = 0;

-: 2х + 4у + 5 z - 4 = 0;

+: 2у - 3 z + 7 = 0.

66. Уравнение плоскости, параллельной оси ОZ и проходящей через точки М₁(3; 1; 0) и М₂(1; 3; 0), имеет вид:

-: 4x + 4у - 11 = 0;

+: х + у - 4 = 0;

-: х + 3у - 4 = 0;

-: x + у - 3 z = 0.

67. Уравнение плоскости, проходящей через точки М₁(3; 3; -1), М₂(0; 2; 5), М₃(1; 1; 1), имеет вид:

+: 5x - 3у + 2z - 4 = 0;

-: 3x - 5у + 4z - 2 = 0;

-: 6x - 4у + z - 3 = 0;

-: 2x + у + 4z - 5 = 0.

68. Расстояние от точки М(5; 1; -1) до плоскости х - 2у – 2 z + 4 = 0 равно:

+: 3;

-: 4;

-: 9;

-: 17,6.

69. Уравнение плоскости, проходящей через начало координат перпендикулярно к двум плоскостям 2x - у + 3z - 1 = 0 и x + 2у + z = 0, имеет вид:

-: 7x - у - 5z + 1 = 0;

+: 7x - у - 5z = 0;

-: 3x + у + 4z - 1 = 0;

-: x - 3у + 2z - 1 = 0.

70. Координаты вектора, параллельного прямой :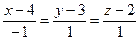

-: а = (4; 3; 2)

+: а = (-1; 1; 1)

+: а = (1; -1; -1)

-: а = (-4; -3; -2)

71. Определить прямую, параллельную прямой :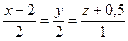

+:

-:

-:

-:

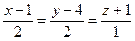
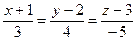
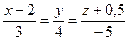
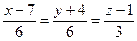
72. Уравнение прямой на плоскости, проходящей через точку А(2;-2) параллельно направляющему вектору а = (2; -3), равно:

+:

-:

-:

-:

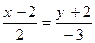
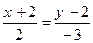
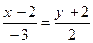
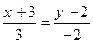
73. Уравнение прямой на плоскости, проходящей через точку А(0; 10) перпендикулярно вектору нормали N = (1; -5), равно:

-:

+:

-:

-:

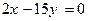
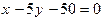
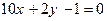
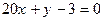
74. Уравнение прямой в пространстве, проходящей через точку А(3; -1; 3) параллельно направляющему вектору а = (2; 1; -3), равно:

+:

-:

-:

-:

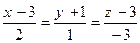
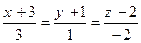
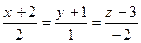
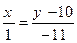
75. Уравнение прямой в пространстве, проходящей через точку M₀(x₀; y₀; z₀) с направляющим вектором a = (a_x; a_y; a_z), имеет вид: 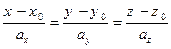. Данное уравнение – это уравнение прямой:

+: каноническое;

-: параметрическое;

-: в отрезках;

-: нормальное.

76. Уравнение прямой линии в пространстве, проходящей через точку 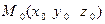с направляющим вектором 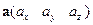, имеет вид: 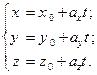. Данное уравнение – это уравнение прямой:

-: каноническое;

+: параметрическое;

-: в отрезках;

-: нормальное.

77. Уравнение прямой в пространстве имеет вид: 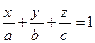. Данное уравнение – это уравнение прямой:

-: каноническое;

-: параметрическое;

+: в отрезках;

-: нормальное.

78. Даны уравнения двух плоскостей в пространстве: 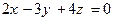; 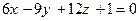. Эти плоскости:

-: перпендикулярны;

+: параллельны;

-: пересекаются;

-: совпадают.

79. Даны уравнения двух плоскостей в пространстве: 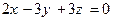; 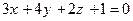. Эти плоскости:

+: перпендикулярны;

-: параллельны;

-: пересекаются;

-: совпадают.

80. Дано уравнение прямой линии в пространстве: 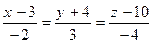и уравнение плоскости 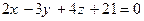. Прямая линия:

-: параллельна плоскости;

+: перпендикулярна плоскости;

-: лежит в плоскости;

-: пересекает плоскость под острым углом.

81. На плоскости дана точка 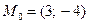. Уравнение прямой, проходящей через данную точку и параллельной вектору 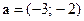, имеет вид:

-: ;

+: ;

-: ;

-: .

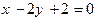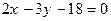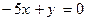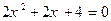82. В пространстве дана точка 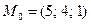. Уравнение прямой, проходящей через данную точку и параллельной вектору 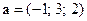, имеет вид:

-: ;

+: ;

-: ;

-: .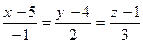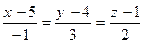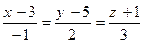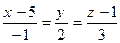