Матрицы. Основные определения.

Введение

В методических указаниях излагаются основные сведения из теории по линейной алгебре, приведено большое количество примеров и задач с подробными решениями. Задачи для практических занятий и самостоятельной работы снабжены ответами.

Предназначены для студентов всех специальностей, изучающих дисциплину "Элементы высшей математики".

Матрицы. Основные определения.

Совокупность 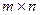чисел (действительных или комплексных), расположенных в виде таблицы, содержащей 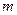строк и 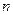столбцов, называют матрицей размерности 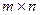. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы принято обозначать прописными буквами А,В, С,…одним из следующих способов:

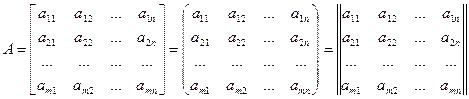(1.1)

Коротко обозначают так: ,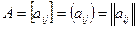

где 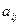- элемент матрицы, индексы i,j определяют положение элемента в матрице. Первый индекс i определяет номер строки, второй j - номер столбца. Матрица, состоящая из одной строки, называется вектор-строкой. Такая матрица имеет вид

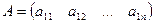
Матрица, имеющая лишь один столбец, называется вектор-столбцом

.

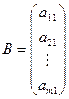Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается

.

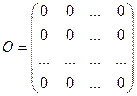Матрица, состоящая из одного числа, отождествляется с этим числом, т.е. любое число можно рассмотреть как матрицу размерности 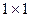, т.е. имеющую одну строку и один столбец.

Квадратной матрицей называется матрица, у которой число строк равно числу столбцов 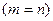, т. е. матрица вида

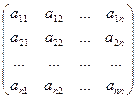(1.2)

В противном случае матрица называется прямоугольной.

Порядком квадратной матрицы называется число ее строк (или столбцов).

Главной диагональю квадратной матрицы (1.2) называется диагональ, идущая из левого верхнего угла в правый нижний. На главной диагонали стоят элементы 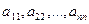, т.е. элементы, у которых номер строки равен номеру столбца .

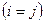Побочной диагональю квадратной матрицы называется диагональ, идущая из левого нижнего угла в правый верхний. На ней стоят элементы .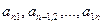

Квадратная матрица, у которой отличны от нуля лишь элементы главной диагонали, называется диагональной.

Если все элементы диагональной матрицы равны единице, то такая матрица называется единичной и обозначается

.

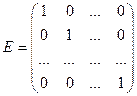Треугольной матрицей называется квадратная матрица, все элементы которой, расположенные по одну сторону от главной диагонали, равны нулю. Различают соответственно верхнюю и нижнюю треугольные матрицы:

,

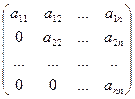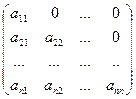
Ненулевая матрица называется ступенчатой, если выполняются следующие условия:

а) первая строка матрицы имеет хотя бы один ненулевой элемент;

б) первый ненулевой элемент любой последующей строки матрицы располагается правее первого ненулевого элемента предыдущей строки;

в) любая строка, состоящая только из нулей, находится ниже всех ненулевых строк.

Две матрицы А=(а_ij) и В=(b_ij) одной размерности называется равными, если для любых i,j выполняются условие: а_ij=b_ij.

Операции над матрицами