Зарядтар жүйесінің алыс қашықтықтағы электростатикалық өрісі.
5.1 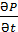 =0;
=0; 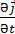 =0 шарттарын қанағаттандыратын, яғни, заряд пен ток тығыздықтары уақытқа тәуелді болмайтын (тұрақты болатын) өріс стационар өріс деп аталады.Мұндай өрістердің потенциалдарының өрнегі (шешімі) кешігуші потенциалдар өрнегімен алынады.Кешігуші птенциалдар өрнегі мына түрде жазылатын: φ(
=0 шарттарын қанағаттандыратын, яғни, заряд пен ток тығыздықтары уақытқа тәуелді болмайтын (тұрақты болатын) өріс стационар өріс деп аталады.Мұндай өрістердің потенциалдарының өрнегі (шешімі) кешігуші потенциалдар өрнегімен алынады.Кешігуші птенциалдар өрнегі мына түрде жазылатын: φ( 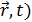 =
= 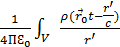 d
d 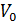 ,
, 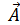 (
( 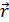 ,t)=
,t)= 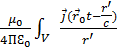 d
d 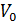 Ал, озушы потенциалдар
Ал, озушы потенциалдар
φ( 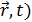 =
= 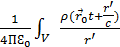 d
d 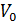
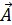 (
( 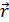 ,t) =
,t) = 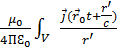 d
d 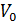
Сонда стационар өріс үшін:
φ( 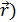 =
= 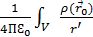 d
d  Стационар өріс үшін Максвелл теңдеу-
Стационар өріс үшін Максвелл теңдеу-
(5.1) →лерінің потенциалдар арқылы жазылуы
 (
( 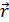 ) =
) = 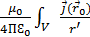 d
d 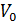
→E=-gradφ- 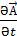
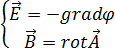
Осыларды ескеріп стационар өріс үшін Максвеллдің дифференциалдық теңдеулерін былайша жазамын.(Электрлік құраушылар мен магнит құраушыларын бөліп жазайық):
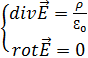 (5.3)
(5.3) 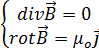 (5.4)
(5.4)
(5.3)-шартты қанағаттандыратын өріс-электростатикалық өріс деп аталады. Дивергенциясы 0-ге тең емес, ал роторы 0-ге тең өріс-потенциалды өріс болып табылады. Олай болса, электростатикалық өріс потенциалды өріс болып табылады. (5.4)-өрнекті қанағаттандыратын өріс-магнитостатикалық(стационар магнит) өріс деп аталады. Дивергенциясы 0-ге тең, ал роторы 0-ге тең емес өріс-құйынды өріс деп аталады. Олай болса, магнитостатикалық өріс құйынды өріс болып табылады.
5.2 Тұрақты электр өрісі 2 жағдайда туындауы мүмкін:
1) Қозғалмайтын зарядтың маңында 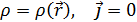
2) Стационар қозғалатын зарядтың айналасында 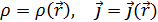
Бірінші жағдайда ток жоқ, мұндай өріс электростатикалық өріс деп аталады. Ал, екінші жағдайда кеңістіктің барық нүктелерінде ток тығыздығы уақытка тәуелді емес,бірдей,мұндай өріс-стационар электр өрісі деп аталады. Стационар электр өрісі үшін 3 және 4 дифференциалдық теңдеулермен қатар мына интегралдық өрнекті де жазуға болады:
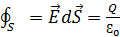 (5.5)Бұл теңдеу Гаусс (Остроградский Гаусс) деп аталады.
(5.5)Бұл теңдеу Гаусс (Остроградский Гаусс) деп аталады.
Электростатикалық потенциалы үшін теңдеу мына түрде жазылады:
(4.7)-өрнектен: 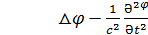 =-
=- 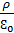 , Стационар өріс үшін :
, Стационар өріс үшін : 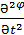 =0,
=0, 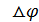 =-
=- 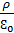 (5.6)-өрнек математикада Пуассон өрнегі деген атпен беріледі. Бұл өрнектін жалпы шешімін табу үшін оның дербес шешіміне сәйкес келетін мынадай бір типті теңдеуді қосып жазуға болады:
(5.6)-өрнек математикада Пуассон өрнегі деген атпен беріледі. Бұл өрнектін жалпы шешімін табу үшін оның дербес шешіміне сәйкес келетін мынадай бір типті теңдеуді қосып жазуға болады:
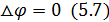 Лаплас теңдеуі
Лаплас теңдеуі
5.3.Практикада нүктелік заряд деген модель жиі қолданылады. Нүктелік заряд:
1. Өрісі қарастырылып отырған нүктеге дейін салыстырғанда өлшемін елемеуге болатын зарядталған дене. 2. Зарядталған дененің туғызатын өрісін анықтау кезінде оның бірлік көлемінің (көлем элементінің) зарядын айтады.Нүктелік зарядтың өрісінің потенциалы мен кернеулігін осы уақытқа дейін қарастырдық, электростатикалық өріс үшін негіз болып табылатынекі нүктелік зарядтың өзара әсерлесу заңын – Кулон заңын Максвелл теңдеулерінен қорытып алған едік.Кулон заңы былайша жазылады: 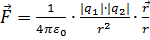 (5.8)Мұндағы:
(5.8)Мұндағы: 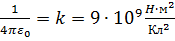 – Кулон тұрақтысы деп аталады.Электростатикалық өрістің кернеулік векторының анықтамасына сәйкес,
– Кулон тұрақтысы деп аталады.Электростатикалық өрістің кернеулік векторының анықтамасына сәйкес, 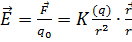 (5.9)Стационар өріс үшін:
(5.9)Стационар өріс үшін: 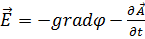 ,
, 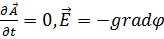 (5.10) (5.9)
(5.10) (5.9) 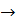 (5.10) қойсақ,
(5.10) қойсақ, 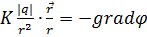 теңдіктің екі жағында
теңдіктің екі жағында 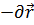 ға көбейтейік
ға көбейтейік 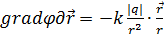 - интегралдайық,,
- интегралдайық,, 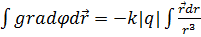 ,
, 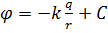 (5.11)Сонымен, 5.11 өрнек электростатикалық өрістің потенциалы болып табылады. Интеграл тұрақтысы С ны табу үшін келесі нормалау шартын пайдаланамыз:
(5.11)Сонымен, 5.11 өрнек электростатикалық өрістің потенциалы болып табылады. Интеграл тұрақтысы С ны табу үшін келесі нормалау шартын пайдаланамыз: 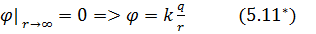
Зарядталған денелер жүйесі үшін егер заряд тығыздығы үздіксіз болса потенциал: 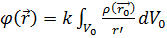 (5.12)
(5.12)
Ал кернеулік 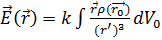
5.4.Кеңістіктің қандай да бір шекті көлемінде үздіксіз таралған зарядтар жүйесінен алыс қашықтықтағы өрісін қарастырайық:
Бұл жағдайда өрістің патенциалы мен кернеулігінің өрнектері жуықтап алыныды және 1 немесе 2 параметірінің көмегімен жүйені сипаттайды.
Патенциалдың жуық мәнін алу үшін 5.12 теңдеудігі 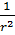 функциясын
функциясын 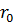 шамасының дәрежесі бойынша қатарга жіктейміз: жазуға ыңғайлы болу үшін x
шамасының дәрежесі бойынша қатарга жіктейміз: жазуға ыңғайлы болу үшін x 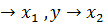 , z
, z 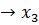 деп белгілеп, ал функцияны
деп белгілеп, ал функцияны 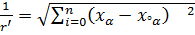 деп белгілеп Тейлор қатарына жіктейміз:
деп белгілеп Тейлор қатарына жіктейміз: 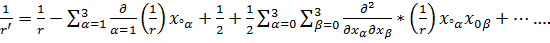 Осы қатарды 1,2 теңдеудің 1/не қойсақ:
Осы қатарды 1,2 теңдеудің 1/не қойсақ: 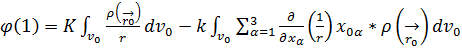 +
+ 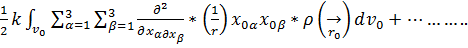
Интеграл белгісінің сыртына идексінде 0 белгісі жоқ, яғни, интегралдың айнымалысы болмайтын шамаларды шығарайық: 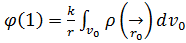 -
- 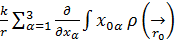 d
d 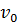 +
+ 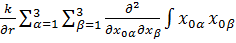 *
* 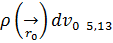
5.13 теңдеудің 1ші құраушысы жүйе патенциалы үшін 0-дік жуықтау д.а
Ал, 5.13-теңдеудің 2ші құраушысы-дипольдік жуықтау д.а.Оны век-қ түрде былайша жазылады:
K grad 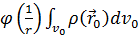
Мұндағы:... 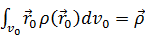 , Егер жүйе n нүктелік зарядтан тұрса, онда дипольдік момент:...
, Егер жүйе n нүктелік зарядтан тұрса, онда дипольдік момент:... 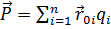
5.13-теңдеудің 3ші құраушысы патенциалдың квадрупольдік жуықтауы деп аталады.
