Проведение эксперимента и обработка результатов

Лабораторная работа № 6.

Определение момента инерции и проверка теоремы

Штейнера методом крутильных колебаний.

Цель работы: изучение колебательного движения крутильного маятника, определение его момента инерции на основе теоремы Штейнера.

I. Основные понятия и определения.

Колебания крутильного маятника являются частным случаем колебаний физического маятника.

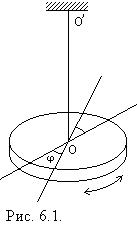
Крутильный маятник представляет собой диск, подвешенный на осевой упругой нити (рис. 6.1). Колебания маятника (диска) происходят в горизонтальной плоскости относительно оси . Согласно основному закону динамики вращательного движения его уравнение движения:

М=Iε, (6.1)

Вследствие упругости нити момент сил М~φ и можно записать 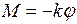. Тогда уравнение (1) приобретёт вид:

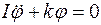или 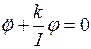. (6.2)

Здесь «·» означает дифференцирование по времени.

Исходя из общего уравнения колебательного движения 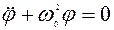, можно предположить, что его решением будет гармоническая функция вида косинус или синус, т.е. маятник будет совершать гармонические колебания с частотой 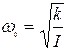, где I — момент инерции маятника. Период колебаний 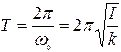. В общем случае, момент инерции тела относительно некоторой оси 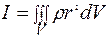, где r — радиус-вектор с началом в центре системы отсчёта, где 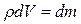- элементарная масса. В случае симметричных тел момент инерции относительно оси, проходящей через центр инерции тела, определяется достаточно просто. Например, для сплошного цилиндра радиуса R, момент инерции равен mR²/2 относительно оси вращения, совпадающей с осью цилиндра.

В общем случае, когда ось вращения не проходит через центр инерции тела, применяют теорему Штейнера, которая гласит, что момент инерции тела I относительно оси, не проходящей через центр инерции, равен моменту инерции тела I₀ относительно параллельной оси, проходящей через центр инерции тела, плюс произведение массы тела m на квадрат расстояния между осями, I=I₀+md².

Методика эксперимента.

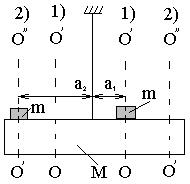Экспериментальная установка представляет собой крутильный маятник с изменяемым моментом инерции (рис. 6.2). Момент инерции изменяется перемещением грузиков массой m, с осей ОО' (1) на оси О'O'' (2) или снятием их с диска. Соответственно, обозначим моменты инерции: диска без грузиков — I₀, диска с грузиками в положении (1) — I₁, диска с грузиками в положении (2) — I₂. Соответственно, периоды колебаний: т₀, т₁, т₂. В общем случае в выражении для периода колебаний 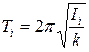, i = 0, 1, 2, неизвестно k.

Рис. 6. 2.

Кроме того, следует учесть теорему Штейнера и момент инерции маятника:

I₁= I₀ + I', I₂= I₀ + I“, (6.3)

где I', I'' – моменты инерции грузиков относительно оси колебаний в положениях (1) и (2), а и r – радиус грузика.

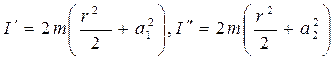. (6.4)

Из этого набора выражений можем получить, что из измерений Т₀ и Т₁ или Т₀ и Т₂ следует, что:

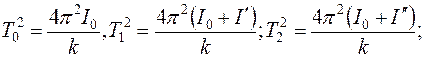. (6.5)

Подставляя 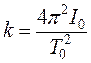в 5, получим:

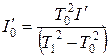или 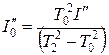, (6.6)

где 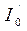и 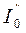- моменты инерции маятника без грузов, полученные из измерений T₀, T₁, T₂, а I’ и I’’ – моменты инерции грузиков, рассчитанные из геометрических и массовых параметров системы.

Таким образом, рассчитав I', I'' можем определить момент инерции свободного диска маятника.

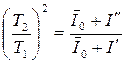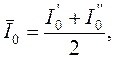Для проверки теоремы Штейнера определим экспериментально и рассчитаем теоретически отношение , где (6.7)

где I - определяется экспериментально по формуле (6.1).

Проведение эксперимента и обработка результатов.

1. Определяем измерением величины r₁, a₁, a₂, m.

2. Последовательно проводим измерения т₀, т₁, т₂. Каждое измерение не менее пяти раз. Для определения периода считаем 10 колебаний t₀. Тогда Т= t₀/10, .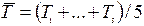

3. Определяем величину I₀' + I₀'' по формулам (6) для I' и I'' (Т₁ и Т₂).

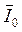= (I₀' + I₀'')/2.

4. Определяем отношение периодов (Т₂/Т₁)² из предыдущих измерений и проверяем расчётом по формуле (7).

5. Результаты заносим в таблицу.

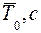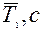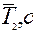			I0', кг/м2	I0'', к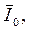г/м2	кг/м2		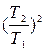(I0 + I')/I0+ I''

а₁= …м, а₂=…м, r=…м, m=…кг, I=…кг/м², I₀=…кг/м².

Контрольные вопросы.

1. Как динамически описать вращательное движение?

2. Какой вид имеет решение основного уравнения динамики вращательного движения, если момент силы носит квазиупругий характер?

3. Что понимается под моментом силы и моментом инерции тела?

4. В чём заключается смысл теоремы Штейнера?

5. Что представляет собой крутильный маятник с переменным моментом инерции?

6. Как определить момент инерции диска крутильного маятника?

7. Как проверить теорему Штейнера?