Устойчивость “обратного” объекта.

Ресурсное ограничение.

Рассмотрим объект управления (6.3), полагая, что помеху измерения удалось исключить. В этом случае его операторное уравнение имеет вид

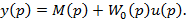(6.7)

Желаемое уравнение для замкнутой системы, соответствующее (6.6), запишем как

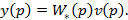(6.8)

Приравнивая правые части выражений (6.7) и (6.8), определим «точное» управляющее воздействие

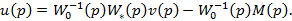(6.9)

Если удастся реализовать закон управления (6.9), то поведение замкнутой системы будет точно соответствовать желаемой передаточной функции (6.6).

Поскольку для реального объекта ресурс управления всегда ограничен, задача синтеза будет разрешима при выполнении первого условия

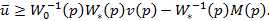
которое и называется ресурсным ограничением.

К сожалению, на практике реализовать управление (6.9) невозможно, так как закон изменения возмущения M(t) неизвестен, кроме границ его изменения, которые и следует подставить для проверки в соотношение (6.10).

Устойчивость “обратного” объекта.

Это условие также предполагает исследование свойств объекта. Изобразим структурную схему, соответствующую выражению для «точного» управляющего воздействия (6.9). Как видим из рис. 6.3, «точный» регулятор включает в себя желаемую передаточную функцию системы и обратную модель объекта. Поскольку 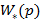всегда имеет полюса с отрицательной вещественной частью, то устойчивость «точного» регулятора определяется устойчивостью обратной модели объекта.

Отсюда следует второе условие разрешимости: задача синтеза будет иметь точное решение, если обратная модель объекта (6.3) 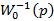устойчива, что соответствует требованию

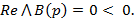(6.11)

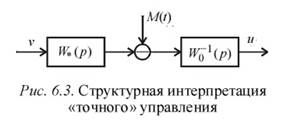
Для разрешимости задачи синтеза необходимо, чтобы все «нули» передаточной функции объекта (корни полинома 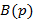) располагались в левой полуплоскости плоскости корней.

Управляемость.

Понятие управляемости используется при проверке условий разрешимости задачи синтеза для линейных систем, поведение которых описывают уравнения состояния.

Рассмотрим условие управляемости для общего класса объектов вида

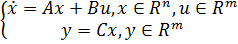(6.12)

Объект (6.12) называется управляемым,если существует ограниченное управляющее воздействие u(t),с помощью которого можно перевести его из начального состояния x(0) в заданное конечное x(T) за конечное время T. Проверяется это условие с помощью критерия управляемости,егоформулировку приведем без доказательства [2, 7]. Объект (6.12) будет

управляем тогда и только тогда, когда матрица управляемости

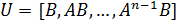(6.13)

имеет полный ранг.

Так как матрица U имеет n строк и n*m столбцов, то критерий управляемости записывается в виде

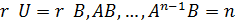(6.14)

Определить, имеет ли матрица полный ранг, можно по соотношению

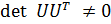, (6.15)

которое легко проверить, например, с помощью пакета Matlab. В случае одноканального объекта (когда m=1) матрица управляемости будет квадратной и критерий (6.14) принимает форму

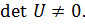(6.16)

Отметим, что задача синтеза будет иметь решение, если объект управляем, т.е. условие управляемости является условием разрешимости задачи синтеза. Однако невыполнение условия (6.14) еще не означает, что такой объект нельзя стабилизировать. В случае, когда r U<n и объект (6.12) не полностью управляем, с помощью специального невырожденного преобразования переменных

его описание можно привести к канонической форме

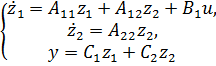(6.17)

Здесь переменные 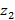характеризуют автономную часть объекта, называемую неуправляемой. Структурная схема такого объекта показана на рис. 6.5. Пунктиром выделена неуправляемая часть объекта, процессы в которой развиваются в силу собственных свойств. Изменить их с помощью управления невозможно, однако переменные 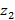влияют на управляемую часть и выходные переменные y. Если неуправляемая часть будет неустойчива, то и весь объект будет не только неустойчивым, но и нестабилизируемым.

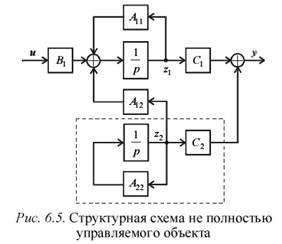
Таким образом, для не полностью управляемого объекта условием разрешимости задачи синтеза является требование устойчивости неуправляемой части.

Наблюдаемость.

Это понятие отражает возможность оценки переменных состояния объекта (6.12) по результатам измерения выходных переменных. Объект называется наблюдаемым,если в любой момент времени можно оценить состояние x по данным измерения выходных переменных y(t)и управляющих воздействий u(t).

Условие проверяется с помощью критерия наблюдаемости,который приводится без доказательства [2, 7]. Объект (6.12) наблюдаем тогда и только тогда, когда матрица наблюдаемости

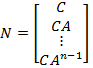(6.18)

имеет полный ранг, т. е.

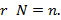(6.19)

Это условие можно проверить по соотношению

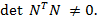
В случае одноканального объекта критерий наблюдаемости (6.19) принимает вид

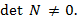(6.20)

Задача синтеза будет иметь решение, если объект наблюдаем, т. е. условие наблюдаемости также является условием разрешимости задачи синтеза.

В случае, когда 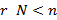, т. е. объект (6.12) не полностью наблюдаем, существует невырожденное преобразование переменных

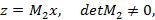
которое позволяет уравнения (6.12) записать в форме

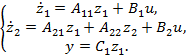(6.21)

Здесь переменные 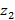характеризуют ненаблюдаемую часть объекта (рис. 6.6).

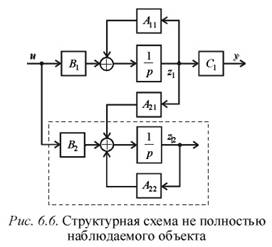
На схеме пунктиром выделена ненаблюдаемая часть. Если она неустойчива, то стабилизировать объект нельзя. Следовательно, в этом случае условие разрешимости задачи синтеза – устойчивость ненаблюдаемой части объекта.