Алгоритм построения взаимной корреляционной функции сообщения и эталонного сигнала

В статье «Корреляция. Автокорреляция» было описано понятие взаимной корреляционной функции (ВКФ). ВКФ часто применяется на практике, например, для синхронизации сообщений. Зачастую формулы, приведенные в данной статье, применить в чистом виде затруднительно.

Рассмотрим ситуацию, когда после обработки входного сообщения с каким-либо видом модуляции (например, по алгоритму, приведенному в статье «DBPSK демодуляция»), мы имеем набор дискретных отсчетов S{s₀, s₁, … , s_n-1 }, соответствующий битовой последовательности двоичных данных, такой что на символ двоичной информации приходится несколько отсчетов (обозначим эту величину как sps(samples persymbol)). Пусть необходимо вычислить ВКФ данного сообщения с заданной эталонной последовательностьE{e₀, e₁, …, e_m-1}, где e_i=±1. Совершенно очевидно, что применять формулы из статьи «Корреляция. Автокорреляция» абсолютно недопустимо, поскольку одному значению из выборки E в соответствие должно быть поставлено несколько значений из выборки S в зависимости от числа отсчетов приходящихся на один символ информации. Мы же хотим построить ВКФ с временным шагом равным периоду дискретизации входного, соответствующему выборке S.

Очевидно, что в соответствие символу эталонной последовательности e_i должно быть поставлено среднее значение отсчетов из выборки S, усреднение должно быть проведено по sps символам (рисунок 1).

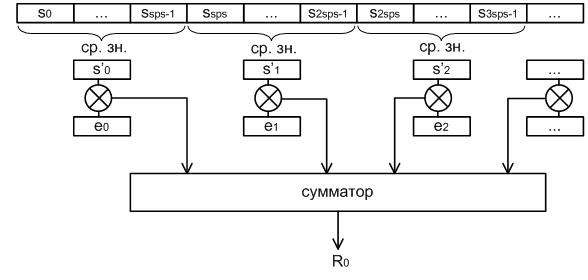
Рисунок 1

После нахождения среднего значения в пределах одного символа получится новая выборка S’. Теперь может быть посчитан коэффициент корреляции r выборок S’ и E по формуле (1) из статьи «Корреляция. Автокорреляция».

Для построения ВКФ необходимо осуществить последовательные сдвиги в исходной выборке S по одному отсчету и на каждом шаге произвести расчет выборки S’ и нового значения ВКФ. Таким образом, формула для вычисления ВКФ по описанному выше алгоритму имеет вид:

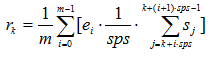,(1)

где k изменяется в диапазоне 0..n-sps-1.

Опишем алгоритм вычисления ВКФ.

S{s₀, s₁, … , s_n-1 } – входная последовательность отсчетов;

n – число отсчетов во входной последовательности;

E{e₀, e₁, …, e_m-1} – эталонная последовательность символов, где e_i=±1

m – число символов эталонной последовательности;

sps – число отсчетов входной последовательности S, приходящихся на один символ информации, переносимой сигналом.

k – индекс итерации.

1. Обработка начинается с первого отсчета выборки S (k = 0).

2. Вычисляются m средних значений (где m - число символов эталонной последовательности E) в пределах символов по выборке S. Усреднение осуществляется по sps отсчетам. Таким образом, производится обработка sps∙m отсчетов выборки S, соответствующей обрабатываемому сообщению. После выполнения получаем m средних значений (массив AVG).

3. Вычисляется коэффициент корреляции

4. Производится инкремент k - сдвиг на один отсчет во входной выборке S и повторяются пункты 2 – 4, до окончания входного массива S.

Данный алгоритм может быть значительно оптимизирован по быстродействию. Обратим внимание на то, что для нахождения среднего значения отсчетов в пределах символа используется суммирование, поэтому вместо массива AVG можно использовать массив SUM, содержащий m сумм отcчетов в пределах символа . Массив SUM полностью может быть вычислен только на первой итерации, при последующих итерациях нет необходимости рассчитывать его полностью, достаточно из каждого элемента вычесть один предыдущий отсчет и прибавить один последующий.

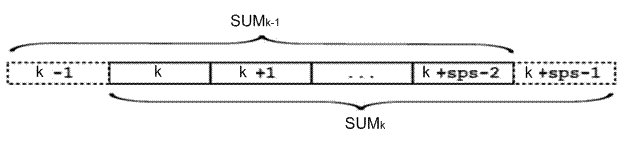
Рисунок 2 – Пояснение к оптимизации нахождения сумм в пределах символа

На рисунке 2 представлено пояснение к алгоритму оптимизации нахождения сумм в пределах символа. Если сумма SUM_k-1 уже известна, то сумма SUM_k может быть вычислена по формуле SUM_k= SUM_k-1 – S_k-1 +S_k+sps-1.

Тогда среднее значение на k-шаге может быть вычислено как AVGk= SUM_k/sps

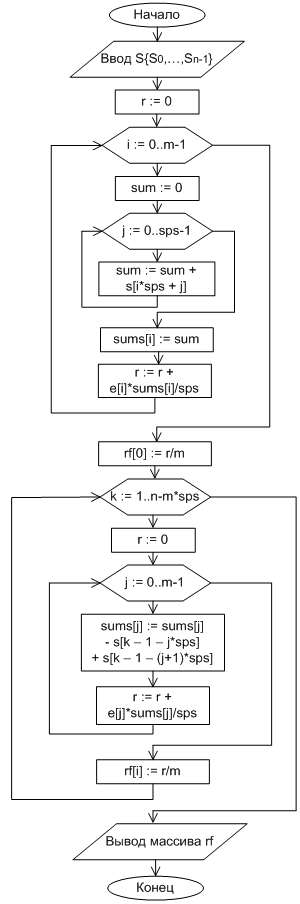
На рисунке 3 представлена блок-схема алгоритма вычисления ВКФ.