Дифференциалдық есептеулердің негізгі теоремалары

Анықтама.Егер нүктесінің бір маңайында теңсіздігі орындалса, онда нүктесін функциясының жергілікті минимум (максимум) нүктесі деп атайды. Жергілікті минимум және жергілікті максимум нүктелері жергілікті экстремум нүктелері деп аталады. Ал осы нүктелердегі функцияның мәні функцияның экстремумы деп аталады. кесіндісінде анықталған функцияның тек қана бір ең үлкен және ең кіші мәндері болады, ал максимумдар және минимумдер бірнеше болуы мүмкін. Функцияның кейбір максимумдары оның минимумдарынан кіші болуы да мүмкін.

Ферма теоремасы. Егер функциясы интервалында дифференциалданатын болса және нүктесінде ең үлкен немесе ең кіші мәнін қабылдайтын болса, онда функцияның туындысы бұл нүктеде нөлге тең, яғни .

Геометриялық мағынасы: функцияның максимум және минимум нүктелерінде жүргізілген жанама өсіне параллель болады.

Ролль теоремасы.Егер функциясы: кесіндісінде үзіліссіз болса, интервалында дифференциалданатын болса және болса, онда ең болмағанда бір нүктесі табылып, болады.

Геометриялық мағынасы: егер теорема шарттары толығымен орындалса, онда кесіндісінде жататын ең болмағанда бір нүктесі табылып, сол нүктеде жүргізілген жанама өсіне параллель болады.

Kоши теоремасы.Егер және функциялары кесіндісінде үзіліссіз болса, интервалында дифференциалданатын болса және , онда ең болмағанда бір нүктесі табылып теңдігі орындалады.

Лагранж теоремасы. Егер функциясы кесіндісінде үзіліссіз болса, интервалында дифференциалданатын болса онда интервалында жататын нүктесі табылып, теңдігі орындалады.

Геометриялық мағынасы: мына қатынас кесіндісінде функциясының графигінің шеткі нүктелерін қосатын хорданың өсінің оң бағытымен жасайтын бұрыштың тангесіне тең, ал нүктесіне жүргізілген жанаманың өсінің оң бағытымен жасайтын бұрышының тангенісіне тең. Лагранж теоремасы бойынша нүктесінде олар өзара тең болады, яғни қиюшы мен жанама параллель болады.

Лопиталь ережесі.Бұл ереже немесе анықталмағандықтарын есептеуге мүмкіндік береді.

Теорема.Айталық, нүктесінің маңайында және функциялары анықталған және дифференциалданатын болсын (нүктенің өзінде бұл шарттар орындалмауы да мүмкін) және , , . Егер шегі бар болса, онда шегі бар болады және мына теңдік орындалады: = . Осы сияқты тұжырымдар , , , , жағдайларда да орынды.

1-мысал. ;

2-мысал. Лопиталь ережесін бірнеше рет қолдануға да болады:

Лопиталь ережесін анықталмағандықтардың мына түрлеріне де қолдануға болады . Ол үшін оларды немесе түрлеріне келтіру керек.

1. Егер көбейтіндісінде ш. а., ал ш.ү. шамалар болса, онда оларды төменгідей түрлендіріп, немесе содан соң Лопиталь ережесін қолданады.

3-мысал. .

2. Екі ш.ү. функциялар айырмасы , яғни анықталмағандығы былай түрлендіріледі бұл өрнекке Лопиталь ережесі қолданылады.

4-мысал.

= .

Әдебиеттер: 1 нег.[238-254], 11 қос. [375-377], [385-390].

Бақылау сұрақтар:

1. Жоғары ретті туындының анықтамасын беріңіз.

2. Жоғары ретті дифференциалдың анықтамасын беріңіз.

3. Ролл теоремасы және оның геометриялық мағынасы.

4. Лагранж теоремасы және оның геометриялық мағынасы.

5. Лопиталь ережесі қандай анықталмағандықтарды есептеуге мүмкіндік береді?

Дәріс.

Дәріс тақырыбы:Туындының көмегімен функцияларды зерттеу және графигін салу

Дәріс жоспары:

§ Функцияның өсу және кему аралықтары.

§ Экстремумның қажетті және жеткілікті шарттары.

§ Функцияның кесіндідегі ең үлкен және еңкіші мәндері.

§ Функцияның дөңестігі, ойыстығы және иілу нүктелері.

§ Функция графигінің асимптоталары.

§ Функцияны зерттеудің жалпы сұлбасы (схемасы) және оның графигін салу.

§ Әдебиеттер.

§ Бақылау сұрақтары.

функциясы 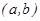аралығында берілсін. Егер кез келген үшін теңсіздігінен ( ) теңсіздігі шығатын болса, онда 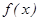функциясы 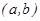аралығында өседі (кемиді) дейді.

Теорема. Егер 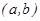аралығында дифференциалданатын 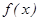функциясының туындысы осы аралықта оң (теріс) болса, онда ол осы аралықта өседі (кемиді). Демек, өсу немесе кему интервалында функцияның туындысы таңбасын өзгертпейді.

1-мысал. функцияның өсу және кему аралықтарын табу керек. Ол үшін функция туындысының таңбасының тұрақтылық интервалдарын анықтаймыз . Бұл квадрат үшмүшеліктің түбірлері x₁=0, x₂=2. Сондықтан, егер аралығында , демек функциясы бұл аралықта кемиді. Ал аралықтарында f'(x)>0, демек бұл аралықтарда функция өседі.

Теорема (экстремумның қажетті шарты).Егер дифференциалданатын функциясының нүктесінде экстремумы бар болса, онда сол нүктеде болады. Осы теоремадан мынадай қорытындыға келеміз: егер нүктесінде функцияның экстремумы бар болса, онда ол нүктеде оның туындысы нөлге тең, не ол нүктеде туындысы болмауы мүмкін. Кері тұжырым әрқашан орындала бермейді. Мысалы, функциясының x₀=0 нүктесінде туындысы , ал бірақ ол нүктеде функция не максимум, не минимум қабылдамайды. функциясының туындысы нөлге айналатын немесе тіпті болмайтын нүктелерді күдікті нүктелер немесе «кризистік» нүктелер деп атайды. Функцияның экстремумын осы күдікті нүктелердің арасынан іздеу керек.

Теорема (экстремумнің жеткілікті шарты). Егер нүктесінде функциясының туындысы нөлге тең болса және нүктесінен өткенде таңбасын өзгертсе, онда нүктесі экстремум нүктесі болады: 1) егер таңба «плюс»-тен «минус»-ке өзгерсе, онда – максимум нүктесі; 2) егер таңба «минус»-тен «плюс»-ке өзгерсе, онда – минимум нүктесі болады.

2-мысал. функцияны экстремумге зерттеп, өсу және кему аралықтарын анықтау керек. Функция туындысы , осыдан , күдікті нүктесін табамыз. нүктесінде функцияның туындысы болмайды, сондықтан ол да күдікті нүкте. Интервалдар тәсілімен f '(x)-тің таңбаларын анықтаймыз. Функция барлық нүктелерде үзіліссіз, жеткіліктілік шарт бойынша максимум нүктесі, ал минимум нүктесі. (–¥, 0) және интервалдарда функция өседі, ал интервалда кемиді Зерттеу нәтижелерін таблицаға жазамыз:

x	(–¥,0)		(0, )		( , +¥)
f '(x)	+	Туындысы жоқ	–		+
f (x)		max		min

Функцияның екінші ретті туындысы қолданылатын экстремумның тағы бір шартын келтірейік.

Теорема. функциясының нүктесінде бірінші және екінші туындылары бар болсын. Егер нүктесінде функциясының бірінші туындысы нөлге тең, яғни болса, ал екінші туындысы нөлден ерекше, яғни болса, онда - экстремум нүктесі болады:

1) егер болса, онда – минимум нүктесі;

2) егер болса, онда – максимум нүктесі болады.

Функцияның кесіндідегі ең үлкен және ең кіші мәндері. Функция өзінің ең үлкен және ең кіші мәндерін экстремум нүктелерінде не кесіндісінің шеткі нүктелерінде қабылдауы мүмкін. Ең үлкен және ең кіші мәндерді табу үшін алдымен функцияның күдікті нүктелерін (не туынды нөлге тең, не туынды жоқ нүктелер) табу керек. Содан соң функцияның күдікті нүктелеріндегі және кесіндінің шеткі нүктелеріндегі мәндерін тауып, олардың ішінен ең үлкен және ең кіші мәндерді іздеу керек.

3-мысал. функциясының кесіндісіндегі ең үлкен жіне ең кіші мәндерін табу керек. Күдікті нүктелерді табамыз:

Осыдан - күдікті нүктелер. Енді функцияның күдікті нүктелердегі және шеткі нүктелердегі мәндерін табамыз: . Сонымен _{үлкен кіші} .