Геометрическое решение игры в смешанных стратегиях (nх2).
В общем случае схема решения игры 2xn или nx2 графическим методом состоит в следующем.
1. Строят прямые, соответствующие стратегиям второго (первого) игрока.
2. Находят две стратегии второго (первого) игрока, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой. Эти стратегии являются активными в оптимальной смешанной стратегии второго (первого) игрока.
3. Находят координаты точки пересечения, тем самым определяя оптимальную стратегию первого (второго) игрока и цену игры.
4. Оптимальную стратегию другого игрока находят, решая систему уравнений, включающую его активные стратегии. На плоскости XY по оси абсцисс отложим единичный отрезок A1A2 (рисунок 5.1). Каждой точке отрезка поставим в соответствие некоторую смешанную стратегию U = (u1, u2). Причем расстояние от некоторой промежуточной точки U до правого конца этого отрезка – это вероятность u1выбора стратегии A1, расстояние до левого конца - вероятность u2 выбора стратегии A2. Точка А1 соответствует чистой стратегии А1, точка А2 – чистой стратегии А2.
В точках А1 и А2 восстановим перпендикуляры и будем откладывать на них выигрыши игроков. На первом перпендикуляре (совпадающем с осью OY) покажем выигрыш игрока А при использовании стратегии А1, на втором – при использовании стратегии A2. Если игрок А применяет стратегию A1, то его выигрыш при стратегии B1 игрока B равен 2, а при стратегии B2 он равен 5. Числам 2 и 5 на оси OY соответствуют точки B1и B2. Аналогично на втором перпендикуляре найдем точки B'1 и B'2 (выигрыши 6 и 4).
Соединяя между собой точки B1 и B'1, B2 и B'2, получим две прямые, расстояние от которых до оси OX определяет средний выигрыш при любом сочетании соответствующих стратегий.
Например, расстояние от любой точки отрезка B1B'1 до оси OX определяет средний выигрыш игрока A при любом сочетании стратегий A1 и A2(с вероятностями u1 и u2) и стратегии B1 игрока B.
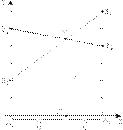
Рисунок 5.1 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока А)
Ординаты точек, принадлежащих ломаной B1MB'2 определяют минимальный выигрыш игрока A при использовании им любых смешанных стратегий. Эта минимальная величина является наибольшей в точке М, следовательно, этой точке соответствует оптимальная стратегия U* = ( 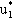 ,
, 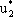 ), а ее ордината равна цене игры v.
), а ее ордината равна цене игры v.
Координаты точки M найдем, как координаты точки пересечения прямых B1B'1 и B2B'2.
Для этого необходимо знать уравнения прямых. Составить такие уравнения можно, используя формулу для уравнения прямой, проходящей через две точки:
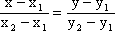 |
Составим уравнения прямых для нашей задачи.
Прямая B1B'1:
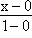 = = 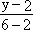 или y = 4x + 2. или y = 4x + 2. |
Прямая B2B'2:
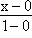 = = 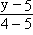 или y = -x + 5. или y = -x + 5. |
Получим систему:
|
Решим ее:
| 4x + 2 = -x + 5, 5x = 3, x = 3/5, y = -3/5 + 5 = 22/5. |
Таким образом, U* = (2/5, 3/5), v = 22/5.
Аналогично решается задача по нахождению оптимальной стратегии игрока B. Разница состоит в том, что находится точка, сводящая к минимуму средний проигрыш, поэтому на рисунке 5.2 рассматривается ломаная A2MA'1.

Рисунок 5.2 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока B)
Найдем координаты точки М.