Теориялық бөлімі. Орнықтылық – бұл жүйенің, оны тепе-теңдік күйінен шығарған әсерді алып тастағаннан кейінгі

Орнықтылық – бұл жүйенің, оны тепе-теңдік күйінен шығарған әсерді алып тастағаннан кейінгі, тепе-теңдіктің бастапқы қалпына қайта келу қасиеті.

Сызықты жүйе орнықтылығының белгілері (шарттары):

а) физикалық – жүйе орнықты, егер өтпелі үрдістің бос құраушысы y_бос(t), уақыт өсуімен нөлге ұмтылса, орнықты емес – егер ол шексіздікке ұмтылса, және бейтарапты, егер ол бір тұрақты шамаға ұмтылса;

б) математикалық – сызықты жүйенің орнықтылығы үшін сипаттамалық теңдеудің барлық түбірлерінде теріс нақты бөлігі болуы (жүйенің барлық полюстері сол жақты болуы керек) қажет және жеткілікті. Егер сипаттамалық теңдеудің қалған сол жақты түбірлерінде бір нөлдік түбір болса, жүйе орнықтылықтың апериодты шекарасында болады, ал егер қалған сол жақты түбірлерінде жұп, таза жорамал (жалған) түбірлері болса, орнықтылықтың тербелісті (периодты) шекарасында болады. Сипаттамалық теңдеу жүйенің беріліс функциясының бөлімінен қалыптасады D(s) = 0.

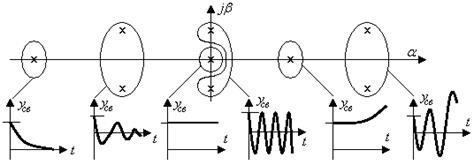
5 – сурет

Түбірдің нақты бөлігіне ( - үрдістің сөну мүмкіндігімен жылдамдығы, ал түбірдің жалған бөлігіне ( - тербеліс қарқынынымен жиілігінің болуы тәуелді [5].

Түбірлерді есептеу мүмкін болмаған кезінде олардың жалған осьіне қатысты жанама белгілері, яғни орнықтылық критерийлері қолданылады. Алгебралық критерийлері (Гурвицтің, Раустың) жүйенің орнықтылығын, сипаттамалық теңдеудің кооэффициенттерінің мәні бойынша, ал жиіліктік критерийлері (Михайловтың, Найквисттің) – жүйенің жиіліктік сипаттамалары бойынша бағалайды.

Михайлов критерийі s = jω сипаттамалық көпмүшені қою арқылы алынған, D(jω) = U(ω) + jV(ω) сипаттамалық функцияны зерттеуге негізделген.

Негізгі тұжырымдама: n-ші ретті жүйе орнықты, егер Михайлов қисығы (=0 болғанда нақты оң жартылай осьтен басталып, ( жиіліктің нөлден плюс шексіздікке дейін өзгеруі кезінде тізбектей, сағат тілі бағытына қарсы комплексті жазықтықтың n ширегін (квадрант) өтсе;

Қосымша тұжырымдама (2 - форма): n – ші ретті жүйе орнықты, егер жұп U(() және тақ V(() функциялары, жиіліктің ( нөлден плюс шексіздікке дейін өзгерісі кезінде тақ функциядан бастап, кезекпен n рет нөлге айналса, яғни олардың түбірлері кезектестіріліп, жиіліктер осьін n рет қиып өтсе. График құру үшін негізгі формада пайдаланылған жиіліктер кестесі қолданылады.

6 – суретте: а) кешенді (комплексті) жазықтықтың ширегін айналып өту кезіндегі тізбегі бұзылған, орнықпаған жүйенің Михайлов қисығы көрсетілген. Егер ( = 0 кезінде, қисық координат басынан басталса, жүйе орнықтылықтың апериодтық шекарасында (сурет 6 б) және егер ( ( 0 кезінде, қисық координат басынан өтсе, орнықтылықтың периодты шекарасында орналасады. U(ω) және V(ω) осьтерін белгілеу әдетте, кешенді жазықтықта жиіліктік сипаттамаларын құру кезінде беріліс функциясының барлық бөлшегіне емес, тек бөліміне ғана пайдаланатынын көреміз.

а б в

6 - сурет

Сипаттамалық теңдеудің оңжақты түбірлерінің санын 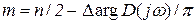формуласы арқылы анықтауға болады. Мұндағы 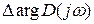– сипаттамалық функция дәлелінің (аргумент) толық өсуі (приращение) (бұрылыстың суммарлық бұрышы).

Бесінші реттік жүйенің векторы D(jω) (сурет 6в), алғашында 3·(π/2) бұрышына бұрылады немесе сағат тілі бағытына қарсы үш ширек (квадрант), кейін 2·(π/2) бұрышына қайтып оралады немесе сағат тілі бағытына қарсы екі ширек (квадрант), соңында 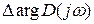= π/2 толық өсіміне сәйкес келеді. Осыдан оң жақты түбір саны: m=5/2–1/2=2 (қисықтың координат осьтерін дұрыс емес қиып өту саны) [3].