Касательная плоскость и нормаль к поверхности. Экстремум функции нескольких переменных

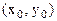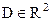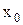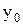Пусть функция z=f(x,y) дифференцируема в точке некоторой области . Рассечем поверхность S, изображающую функцию z, плоскостями x= и y= . Плоскость x= 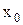пересекает поверхность S по некоторой линии 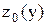, уравнение которой получается подстановкой в выражение исходной функции z=f(x,y) вместо х числа 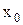. Точка 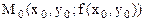принадлежит кривой 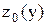. В силу дифференцируемости функции z в точке 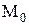функция 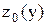также является дифференцируемой в точке y= 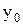. Следовательно, в этой точке в плоскости x= 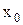к кривой 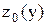может быть проведена касательная 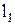. Построим касательную 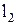к кривой 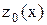в точке x= 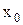. Прямые 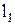и 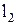определяют плоскость 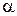, которая называется касательной плоскостью к поверхности S в точке 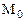. Составим ее уравнение. Так как плоскость 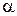проходит через точку 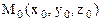, то ее уравнение может быть записано в виде А( 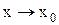) + В( 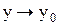) + С( 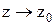)=0, которое можно переписать так: 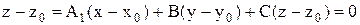(разделив уравнение на –С и обозначив А/-С= 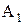, В/-С= 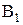). Найдем 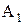и 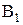. Уравнения касательных имеют вид: 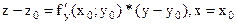; 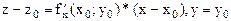соответственно. Касательная 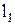лежит в плоскости 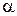. . 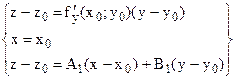В итоге 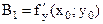. Следовательно, 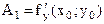. Искомое уравнение касательной плоскости: 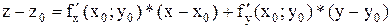. Прямая, проходящая через точку 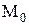и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью. Каноническое уравнение нормали: .

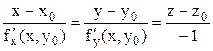Экстремум ф-ции нескольких переменных. Теорема(необходимые условия экстремума): Если в точке N( 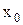, 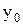) дифференцируемая функция z=f(x,y) имеет экстремум, то ее частные производные в этой точке равны нулю: 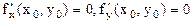. Док-во: Зафиксируем одну из переменных. Положим, y= 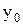. Тогда получим ф-цию 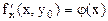одной переменной, которая имеет экстремум при x- 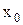. Следовательно, согласно необходимому условию экстремума функции одной переменной, 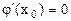, т.е. 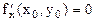. Замеч.: ф-ция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Точка, в которой частные производные первого порядка функции z=f(x,y) равны нулю, т.е. 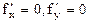, называется стационарной точкой функции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Теорема(достаточное условие экстремума): Пусть в стационарной точке 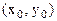и некоторой ее окрестности функция F(x,y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке 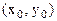значения 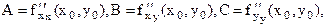обозначим 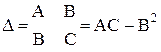. Тогда: 1.Если 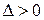, то функция f(x,y) в точке 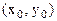имеет экстремум: максимум, если A<0, минимум, если A>0; 2.Если 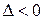, то функция f(x,y) в точке 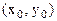экстремума не имеет. В случае 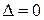экстремум в точке 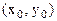может быть, может не быть. Необходимы дополнительные исследования.