Приближенная теория анизотропной пластинки, учитывающая явления поперечного сдвига

Вышеприведенная теория справедлива для решения плоских задач о напряженно-деформированном состоянии тонких слоистых анизотропных (изотропных) оболочек (пластин), т.е. без учета явления поперечного сдвига. Такие подземные объекты как непосредственная кровля, охранные сооружения, стволы и т.д. могут быть рассмотрены в виде трехмерных систем, как наиболее адекватным к реальным. Поэтому приведем основное уравнение для определения напряженно-деформированного состояния, в частности анизотропных пластины, учитывающее явление поперечного сдвига.

Для ортотропной пластинки:

а) расстояния по нормали ( 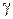) между двумя точками пластинки до и после деформации остаются неизменными;

б) нормальные напряжения 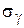на площадках, параллельных срединной плоскости, могут быть пренебреженны по сравнению с прочими напряжениями;

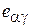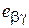в) при определении деформаций и считаем, что касательные напряжени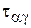й и 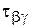не отличаются от соответствующих напряжени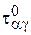й ( и 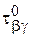), найденных при наличии гипотезы недеформируемых нормалей, т.е. от соответствующих напряжений классической теории изгиба анизотропных пластинок.

В силу принятых предположений для напряжений имеем

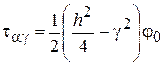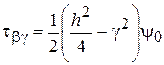, , (2.70)

,

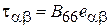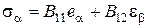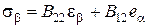, , (2.71)

где

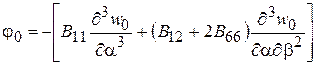, (2.72)

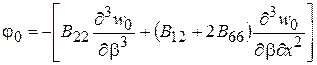, (2.73)

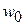– нормальное перемещение соответствующей ортотропной пластины, найденное при наличии гипотезы недеформируемых нормалей. Здесь предполагается , .

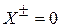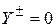Для перемещений, деформаций и напряжений имеем

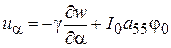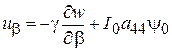, , (2.74)

для нормального перемещения имеем

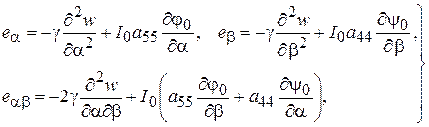(2.75)

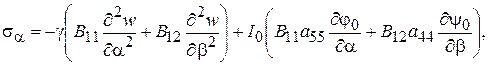(2.76)

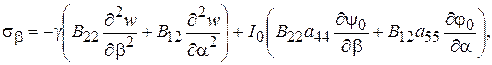(2.77)

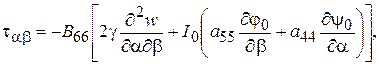(2.78)

где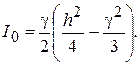

Для внутренних сил и моментов получим

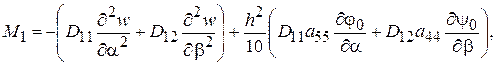(2.79)

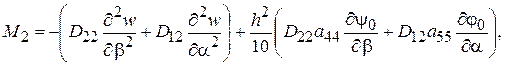(2.80)

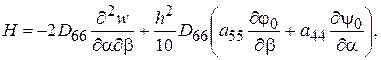(2.81)

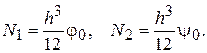(2.82)

Разрешающее дифференциальное уравнение относительно одной искомой функции :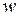

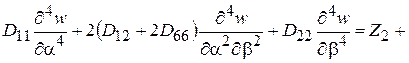
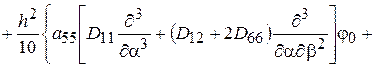
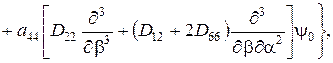(2.83)

где .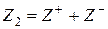

Запишем его в несколько преобразованном виде

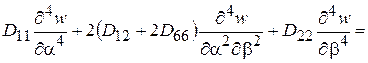
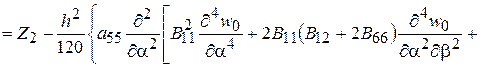
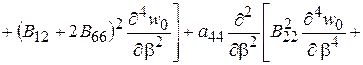
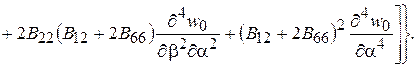(2.84)

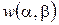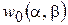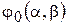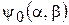Таким образом, в этом варианте теории задача поперечного изгиба ортотропной пластинки свелась к определению лишь функции (функция и тем самым функция и известны из классической теории изгиба анизотропной пластинки). Эта функция удовлетворяет дифференциальному уравнению четвертого порядка (2.84) или (2.83), которые своими левыми частями ничем не отличаются от левой части известного уравнения классической теории изгиба анизотропной пластинки, и граничным условиям, которые тоже ничем не отличаются от граничных условий классической теории. Для примера приведем однородные граничные условия для четырех случаев (см. 2.8):

а) свободный край

;

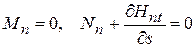б) шарнирно закрепленный край

;

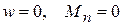в) заделанный край (закреплен элемент срединной поверхности)

;

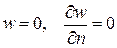г) заделанный край (закреплен вертикальный элемент края)

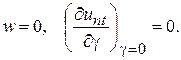
В случае, когда пластинка цилиндрически анизотропна, по предлагаемой здесь теории имеем следующие расчетные формулы и уравнения:

основные расчетные напряжения

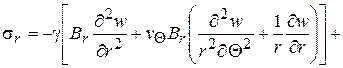
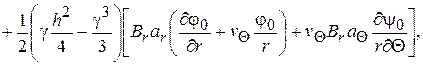(2.85)

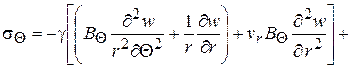
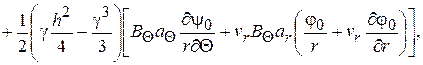(2.86)

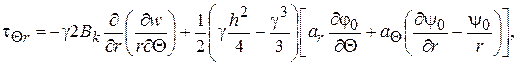(2.87)

внутренние изгибающие и крутящие моменты

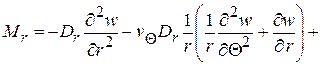
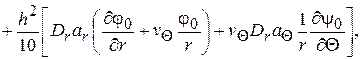(2.88)

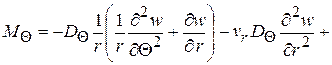
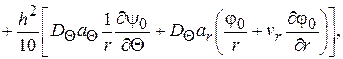(2.89)

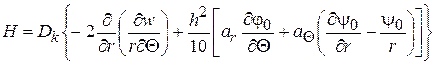(2.90)

и наконец, разрешающее уравнение задачи

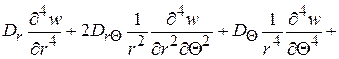
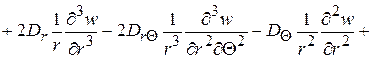
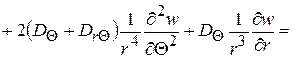
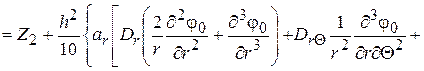
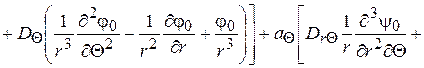
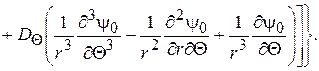(2.91)

Во всех этих формулах и уравнениях для функци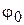й и 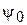имеем

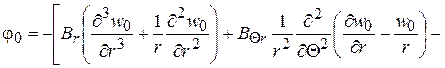
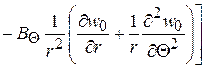, (2.92)

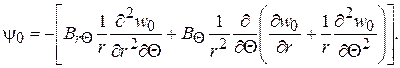(2.93)

Предлагаемую здесь теорию можно несколько улучшить. Дело в том, что, не вводя никаких существенных осложнений, можно освободиться от предположения о пренебрежительности 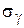по сравнению с прочими напряжениями; тогда для расчетных напряжений получим

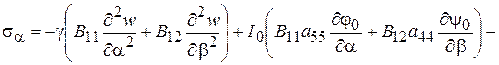
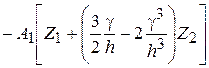, (2.94)

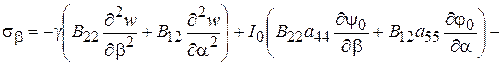
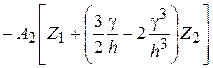, (2.95)

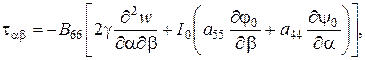(2.96)

где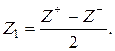

Для моментов и поперечных сил имеем

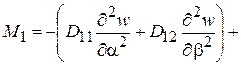
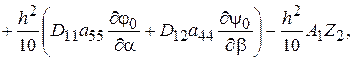(2.97)

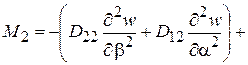
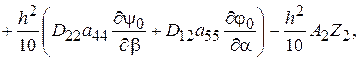(2.98)

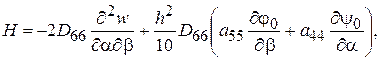(2.99)

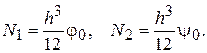(2.100)

и, наконец, разрешающее дифференциальное уравнение задачи

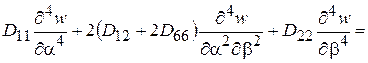
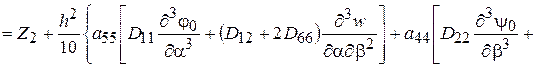
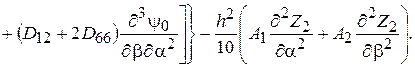(2.101)

Рассматривая формулы для расчетных величин (5.27)-(5.33) и разрешающее уравнение (5.34)уточненного варианта теории, замечаем, что они от соответствующих формул (5.8)-(5.14) и разрешающего уравнения (5.16) неуточненной теории отличаются лишь членами, которые содержат множител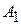и и 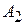, которая имеют вид

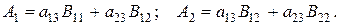(2.102)

В вышеприведенных уравнениях приведены механические характеристики: модули упругости Е и коэффициенты Пуассона 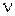для сплошных сред. Однако горные породы обладают трещиноватостью, поэтому ее учет представляет теоретический и практический интерес, что изложено в следующем разделе.