Решение системы уравнений методом Зейделя

Предполагая, что a_ii ≠ 0 разрешим новое уравнение системы (1) относительно x₁, второе – относительно x₂,…, n-ое уравнение – относительно x_n. В результате получим:

x₁ = β₁ - α₁₂x₂ - α₁₃x₃ - ... - α_1nx_n

x₂ = β₂ - α₂₁x₁ - α₂₃x₃ - ... - α_2nx_n

x_n = β_n - α_n1x_n - α_n3x₃ - ... - α_nn-1x_n-1

где β_i = b_i/a_ii; α_ij = a_ij/a_ii при i ≠ j; α_ii = 0

Известно начальное приближение: x⁰ = (x⁰₁, x⁰₂, ..., x⁰_n).

Основная идея заключается в том, что при вычислении (k+1)-го приближения неизвестной x_i учитываются уже вычисленные ранее (k+1) - приближение неизвестных x₁, x₂, ..., x_n.

Итерационная схема имеет вид:

x^k+1₁ = β₁ - ∑α_1jx^k_j

x^k+1₂ = β₂ - α₂₁x^k+1₁ - ∑α_2jx^k_j

x^k+1_i = β_i - ∑α_ijx^k+1₁ - ∑α_2jx^k_j

Приведем к виду:

x₁ = 0.14+0.08x₂+0.296x₃

x₂ = 0.4815+0.1852x₁+0.3287x₃

x₃ = -0.3506-0.6118x₁-0.2935x₂

Покажем вычисления на примере нескольких итераций.

N = 1

x₁ = 0.14 - 0 • 0.08 - 0 • 0.296 = 0.14

x₂ = 0.4815 - 0.14 • 0.1852 - 0 • 0.3287 = 0.4556

x₃ = -0.3506 - 0.14 • (-0.6118) - 0.4556 • (-0.2935) = -0.1312

N = 2

x₁ = 0.14 - 0.4556 • 0.08 - (-0.1312) • 0.296 = 0.1424

x₂ = 0.4815 - 0.1424 • 0.1852 - (-0.1312) • 0.3287 = 0.4982

x₃ = -0.3506 - 0.1424 • (-0.6118) - 0.4982 • (-0.2935) = -0.1172

N = 3

x₁ = 0.14 - 0.4982 • 0.08 - (-0.1172) • 0.296 = 0.1348

x₂ = 0.4815 - 0.1348 • 0.1852 - (-0.1172) • 0.3287 = 0.495

x₃ = -0.3506 - 0.1348 • (-0.6118) - 0.495 • (-0.2935) = -0.1228

Остальные расчеты сведем в таблицу.

N	x1	x2	x3	e1	e2	e3
	0.14	0.456	-0.131	0.14	0.456	0.131
	0.142	0.498	-0.117	0.0024	0.0427	-0.014
	0.135	0.495	-0.123	-0.0076	-0.0032	0.0056
	0.137	0.497	-0.121	0.0019	0.0015	-0.0016
	0.136	0.496	-0.122	-0.0006	-0.0004	0.0005

Таким образом, мы получаем систему:

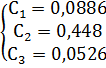
Подставим полученные значения С в уравнение

Ѱ(X_i)=C­_1­* Ѱ­_1­(X)+C­_2­* Ѱ­­_2­(X)+ C_3­* Ѱ­_3­­­(X)

Ѱ(X₁)=-0,0886-0,403+0,535=0,321

Ѱ(X₂)=0,313

Ѱ(X₃)=0,335

Ѱ(X₄)=-0,037

Ѱ(X₅)=-0,030

Подставим значения Ѱ(X_i) в уравнение Ϭ=y(X_i)- Ѱ(X_i) и найдем максимальное отклонение (значение аппроксимации)

Ϭ₁=-0,62

Ϭ₂=0,18

Ϭ₃=-0,09

Ϭ₄=-0,110

Ϭ₅=0,061

Ϭ_max=0,18 при X₂=-0,30

Схема алгоритмов

1. Схема алгоритма подпрограммы выбора функции (vibor):

Начало

Ввод ( k, x )

нетда

k=1

да

k=2Ввод ( sinx )

нет

Ввод ( 1 ) Ввод ( cosx )

Конец

2. Схема алгоритма подпрограммы расчёта коэффициентов (аb):

m = 3

n = 5

Начало

Ввод ( x[n],[y] )

i = 0; i < m, i++ // цикл по строкам для

расчёта матрицы a и вектора b

j = 0, j < m, j++ // цикл по столбцам для расчёта

матрицы a

Sum = 0 // исходное значение переменной

Sum

J = 0, J < n, J++ // цикл расчёта элементов

матрицы а

Sum = Sum+vibor (( i, x [J] ) * vibor ( j, x [J] ))

J // конец цикла J

a [i] [j] = Sum // присваивание ij элементу его

значения Sum

j // конец цикла j

Sum = 0//исходное значение переменной

Sum

J = 0, J < n, J++//цикл расчёта элементов вектора

b

Sum = Sum + vibor ( i,x [J] * y [J])

J // конец цикла J

b [i] = Sum //присваивание i элементу его

значения Sum

i//конец цикла i

Вывод (а [m] [m], b [m])

Конец

3. Схема алгоритма подпрограммы вывода матрицы (vivodmatr):

Начало

Ввод (а [m] [m])

i = 0, i < m, i++ // цикл по строкам для вывода

элементов матрицы а

j = 0, j < m, j++ // цикл по столбцам для вывода

элементов матрицы а

Вывод (а [i] [j] )

j // конец цикла j

i // конец цикла i

Конец

4. Схема алгоритма вывода вектора (vivodvek):

Начало

Ввод ( b [m] )

i = 0, i < m, i++ // цикл по строкам для

вывода элементов вектора b

Вывод ( b [i] )

i

Конец

5. Схема алгоритма подпрограммы метода Зейделя (Zeidel):

Начало

// Прямой ход

Ввод ( A,X₀,B, eps,N ) // цикл исключения

переменной с номером i

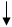M=1(1)N

X(M)=X0(M)

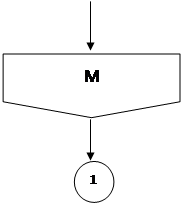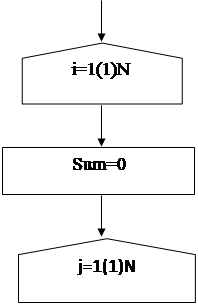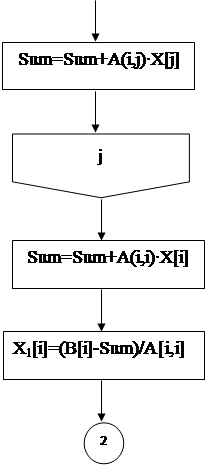6. Подпрограмма расчёта f [i], g [i] и вывода результатов в виде таблицы (tabl):

m = 5

n = 5

Начало

Ввод ( x [n], y [n], x [m], g [n] )

// цикл расчёта

i = 0, i < n, i++ f [i], g [i] и вывода

таблицы результатов

f [i] = c [o] + c [1] * x [i] + c [2] * x [i] * x [i] //считаю найденную

аппроксимирующую

функцию в точках

g [i] = y [i] – f [i] // считаем погреш-

ность аппроксимации

Вывод ( x [i], y [i], f [i], g [i] )

i // конец цикла i

Конец

7. Подпрограмма расчёта и вывода z (approksi):

Начало

Ввод ( g [n] )

//начальное значение

z = 0 качества аппроксимации

//цикл расчёта качества

i = 0, i < n, i++ аппроксимации

//качество аппроксимации

z = z + g [i] *g [i]равно сумме квадратов

погрешностей аппроксимац.

i

Вывод ( z )

Конец

8. Подпрограмма поиска и вывода максимального отклонения по модулю ( otklonenie):

n = 5

Начало

Ввод ( G [n], x [n] )

// пусть первая погрешность

g = | g [0] | аппроксимации максимальна

по модулю

max = 0

// цикл поиска максимального

по модулю отклонения

i = 0, i < n, i++ // если текущее отклонение

больше максимального

да

| G [i] | > g

// текущее

G = | g [i] | отклонение

нетстановится

max = i максимальным

i // конец цикла i

Вывод ( z )

Конец

9. Схема алгоритма основной программы:

Начало

// цикл ввода исходных

i = 0, i < n, i++ значений x и y

Ввод x [i]

Ввод y [i]

i // конец цикла i

// расчёт коэффициента

аb ( x, y, a, b ) нормальных уравнений

(матрицы a и вектора b)

vivodmatr ( a ) // вывод матрицы a

// вывод вектора b

vivodvek ( b)

gauss ( a, b, c) // решение СЛУ (c1, c2, c3)

vivod c ( c ) // вывод c1, c2, c3

Вывод ( f ) // вывод искомой

аппроксимирующей

функции

// вывод результатов в

tabl ( x, y, c, g ) таблице

// расчёт и вывод качества

approksi ( g ) аппроксимации

// расчёт и вывод

otklonenie ( g, x ) максимального по модулю

отклонения

Конец

10. Вывод значений с:

m = 3

Начало

i = 0 (i), i < m, i++

Вывод ( с [i] )

i

Конец