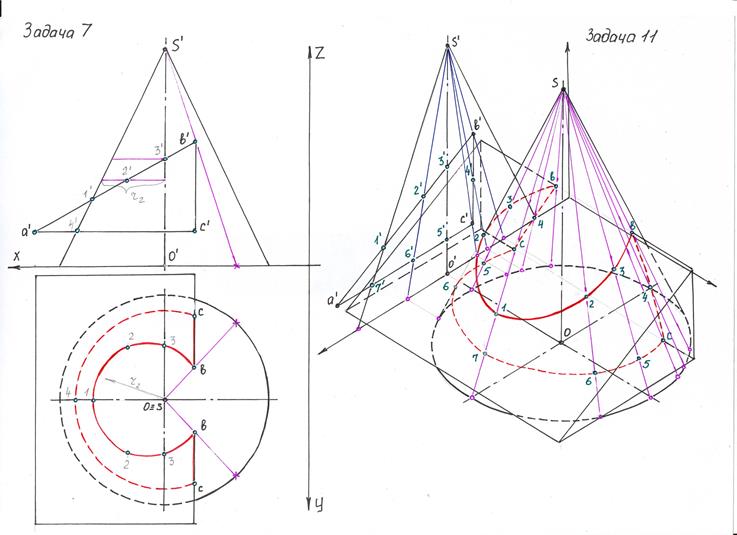
Задача 7. Принцип решения

1. Строим проекции конуса и призмы по заданным координатам.

2. Отмечаем точки пересечения очерковых образующих – 1^/ и 4^/ , затем точку пересечения призмы с осью конуса – 3^/. Так как грань призмы а^/-с^/ расположена параллельно оси ох, то точки, принадлежащие ей, будут лежать на окружности. Грань а^/-b^/ наклонная, следовательно на горизонтальной плоскости проекций точки, лежащие на ней, будут лежать на эллипсе. Для точности построения линии пересечения отмечаем дополнительную точку 2^/.

3. Строим точки на горизонтальной плоскости проекций: точки 1 и 4 будут лежать на горизонтальной оси конуса, так как они лежат на очерковой образующей конуса. Точку b^/ фиксируем с помощью вспомогательной образующей s^/-x, строим образующие на второй плоскости проекций (s-x) и сбрасываем на них точки b. Точки 2^/ и 3^/ находим с помощью вспомогательных плоскостей, рассекающих конус параллельно основанию конуса, в сечении получаем окружности. Измеряем радиус от вертикальной оси конуса до очерковой образующей. Строим вспомогательные окружности на горизонтальной плоскости проекций из центра основания конуса, и сбрасываем точки на соответствующую окружность.

4. Соединяем точки в той последовательности, как они обозначены на гранях призмы (1^/-2^/-3^/-b^/-c^/-4^/). Определяем видимость лини пересечения. Если смотреть на конус сверху, то его боковая поверхность будет видна полностью. Если смотреть сверху на призму, то грань а^/-с^/ будет невидимой, а остальные видимыми. Следовательно, линия 1-2-3-b-c будет видимой, а линия с-4 будет невидимой.

Задача №8.

Построить линию пересечения фронтально - проецирующего цилиндра вращения с поверхностью наклонного конуса с круговым основанием.

Данные к задаче в таблице 6.

Указания к решению задачи №8.

По координатам, взятым из таблицы 6, строят коническую поверхность и цилиндр вращения. На фронтальной плоскости проекций линия пересечения цилиндра и конуса уже представлена в виде очерка цилиндра (окружности). Задача сводится к построению горизонтальной проекции линии пересечения. Для решения удобно воспользоваться фронтально – проецирующими секущими плоскостями, проходящими через вершину конуса. При решении задачи обязательно следует показать построение точек, определяющих границы видимости кривой пересечения и точки касания кривой пересечения с очерковыми линиями заданных поверхностей. Все основные невидимые линии показывают штриховыми линиями. Все линии вспомогательных построений должны быть показаны четкими тонкими линиями.

Таблица 6. Данные к задаче №8

№ вар	XО	YО	ZO	XS	YS	ZS	XE	ZE	RК	Rц

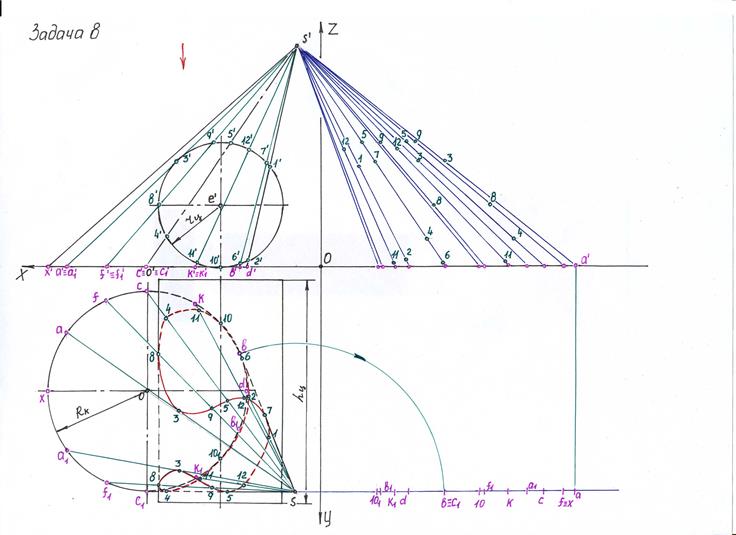
Задача 8 Принцип решения:

1. По координатам строим проекции точек О,О^/ и S, S^/. От точки О^/ откладываем радиус - R основания конуса на фронтальной плоскости проекций и соединяем полученные точки с вершиной конуса S^/, получим проекцию конуса. На горизонтальной плоскости проекций чертим окружность с центром в точке О и из точки S проводим касательные к окружности (основание конуса), получили вторую проекцию конуса.

2. Строим по координатам точку е^/ на фронтальной плоскости проекций и из полученной точки чертим окружность радиусом – r_ц, получим проекцию фронтально – проецирующего цилиндра. На горизонтальной плоскости проекций строим ось цилиндра параллельно оси ОY . Основания цилиндра вычерчиваем перпендикулярно к оси цилиндра и располагаем их за проекцией конуса, при этом длина цилиндра будет приблизительно равна 4 r_ц.

3. Отмечаем характерные точки пересечения очерковых образующих конуса и цилиндра на фронтальной плоскости проекций. Это точки 1^/, 2^/ и 10^/. Далее проводим касательную к окружности цилиндра и восстанавливаем к касательной перпендикуляр, проходящий через центр окружности, полученную точку отмечаем точкой 3^/. Так как на горизонтальной плоскости проекций необходимо будет показать видимость линии пересечения, то определяем границы видимости для конуса. Границами видимости будут крайние очерковые образующие конуса, отмечаем точки касания образующих с основанием конуса, при этом помним, что точка касания лежит на перпендикуляре, восстановленном из центра окружности к образующей. Отмечаем точки b и c₁. дальше находим проекции этих точек на фронтальной плоскости проекций, основание конуса лежит на оси ОХ , следовательно поднимаем проекции точек на ось ОХ и соединяем их с вершиной конуса S^/ получим образующие b^/-S^/и c₁^/-S^/. Построенные образующие пересекают очерк цилиндра в точках: 4^/, 5^/, 6^/ и 7^/.

4. На горизонтальной плоскости проекций необходимо учесть видимость цилиндра, это левая образующая цилиндра. На фронтальной плоскости проекций проводим вспомогательную образующую конуса через точку пересечения окружности основания цилиндра с горизонтальной осью, отмечаем точки 8^/ и 9^/.

5. Остается большой промежуток между точками 4^/ и 10^/ . Строим промежуточную образующую s^/-к^/ произвольно и отмечаем точки 11^/ и 12^/.

6. Строим все образующие на горизонтальной плоскости проекций и сбрасываем на них соответствующие точки. Например, строим образующую а-S (их будет две) и проецируем на них точки 3. Аналогично достраиваем все точки.

7. Точки на горизонтальной плоскости проекций соединяем в том порядке, в каком они обозначены на фронтальной проекции цилиндра, т.е. 1-7-12-5-9-3-8-4-11-10-6-2-6-10-11-4-8-3-9-5-12-7. Определяем видимость кривой: смотрим на фронтальной плоскости проекций (по направлению взгляда, обозначенного стрелкой) все точки лежащие над горизонтальной осью цилиндра будут видимыми (1^/,7^/,12^/,5^/,9^/,3^/,8^/), а под ней – невидимыми. Но на горизонтальной плоскости проекций необходимо учитывать границы видимости конуса – это точки 7 и 5. Тогда видимыми будут следующие части кривой: 8-3-9-5-12-7 и 8-3-9-5.

Задача №9.

Построить развертку наклонного конуса и развертку цилиндрической поверхности с нанесением на развертках их линии пересечения.

Указания к решению задачи №9.

Исходные данные для решения задачи берутся из задачи №8. Для построения развертки наклонного конуса на поверхности конуса проводят ряд образующих и находят их истинные длины. Эти построения следует выполнить тонкими линиями на чертеже при решении задачи №8. Затем, методом раскатки, используя истинные длины образующих и хорды на основании конуса, строят развертку конической поверхности. Далее наносят линию пересечения конуса с цилиндром. Развертка цилиндра представляет из себя прямоугольник с размерами равными длине цилиндра и длине основания окружности цилиндра. На развертке цилиндра также показывают линию пересечения конуса с цилиндром. Все построения показать тонкими линиями. Точки на линии пересечения должны иметь те же обозначения, что и на проекционном чертеже.

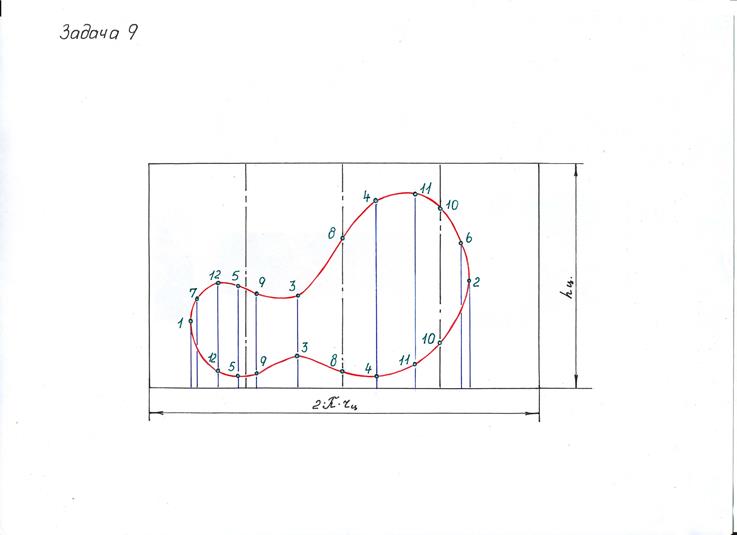
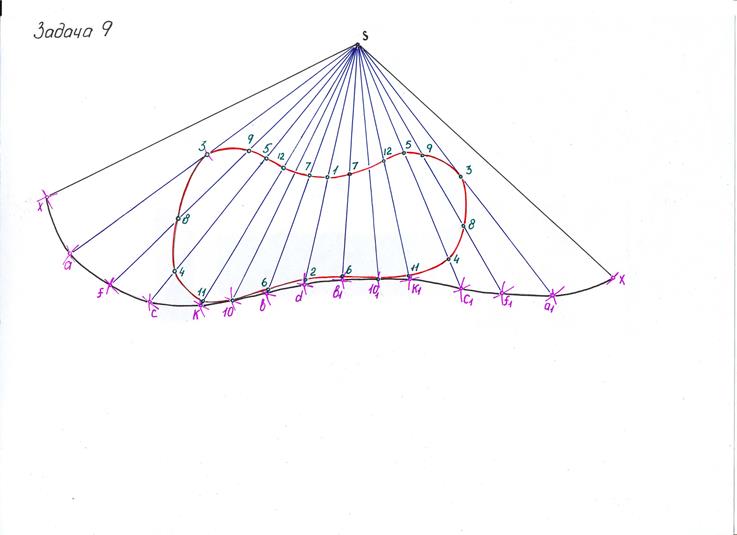
Задача 9 Построить развертки боковой поверхности конуса и цилиндра и нанести на них линию их пересечения.

1. Для построения 9 задачи необходимо найти натуральные величины образующих конуса. Для этого из точки S (в задаче 8) проводим прямую параллельную оси ОХ и методом вращения разворачиваем все образующие конуса. Так как при развертывании основания конуса в окружность вписывают n-угольник, то необходимо следить, чтобы угол между точками на окружности не превышал 30⁰, поэтому между точками а и а₁ отмечаем точку х и между точками 10₁ и d отмечаем точку b₁.

2. Последовательно поднимаем точки на ось ОХ, так как все точки находятся на основании конуса, и соединяем их с вершиной s^/. Полученные образующие и есть натуральные величины. Параллельно оси ОХ переносим на каждую свои точки. Если образующих две, то на каждую переносим одноименные точки, например, образующие а-s^/ и a₁-s^/ будут содержать точку 3.

3. Строим развертку конуса: проводим прямую произвольно, отмечаем на ней точку s. От нее откладываем по прямой натуральную величину образующей х-s^/. Так как на горизонтальную плоскость проецирования основание конуса проецируется без искажения, то расстояние между образующими берем с основания конуса. Измеряем расстояние х-а₁ и откладываем на развертке от точки х, а затем замеряем натуральную величину образующей s^/-a₁ и из вершины s проводим дугу до пересечения с дугой х-а₁. Полученную точку пересечения дуг обозначаем а₁. Полученную точку а₁ соединяем с s и откладываем на ней натуральную величину s^/ -3. Так выстраиваем все точки, последовательно двигаясь по основанию конуса. Завершаем той же образующей, с какой начинали строить. Точки основания замыкаем плавной линией, и точки линии пересечения также замыкаем между собой.

4. Строим развертку цилиндра. Боковая поверхность цилиндра представляет собой прямоугольник длиной 2pR. Высота прямоугольника равна длине цилиндра на горизонтальной плоскости проекций. Делим развертку на 4 равные части и переносим положение точек на цилиндре, измеряя расстояние между ними на фронтальной проекции основания цилиндра. Желательно чтобы расстояние между точками также укладывалось в угол = 30⁰, если угол больше, то для точности построения разбиваем дополнительными точками. Положение точек линии пересечения определяем на горизонтальной проекции цилиндра, измеряя расстояние от нижнего или верхнего основания цилиндра до точки. Измерять необходимо перпендикулярно к основанию цилиндра. Полученные точки соединяем между собой.

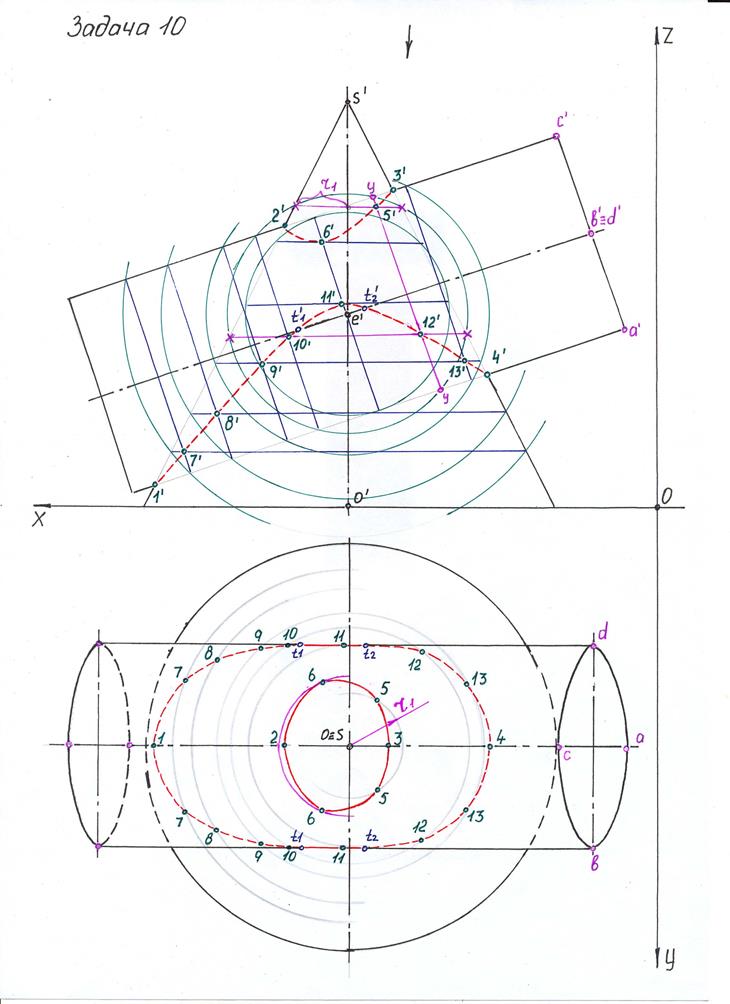
Задача №10.

Методом сфер построить линию пересечения конуса и цилиндра. Данные к задаче в таблице 7.

Указания к решению задачи №10.

По координатам строят поверхности конуса и цилиндра. Определяют точку пересечения осей конуса и цилиндра. Из точки пересечения осей как из центра проводят сферу произвольного радиуса. Сфера пересекает обе поверхности по окружностям, плоскости которых перпендикулярны осям поверхностей конуса и цилиндра. На пересечении этих окружностей, вырождающихся в прямые линии, находят общие точки для поверхностей конуса и цилиндра. Далее строят горизонтальную проекцию линии пересечения и определяют видимость поверхностей.

Таблица 7. Данные к задаче №10.

№ вар	XО	YО	XЕ	ZЕ	RK	Rц	aО

Задача 10 Принцип решения:

1. По заданным параметрам выстраиваем проекции конуса и цилиндра, при этом на горизонтальной проекции ось цилиндра проходит параллельно оси ОХ и совпадает с горизонтальной осью основания цилиндра. Так как цилиндр расположен под углом, то правое основание будет видимым в виде эллипса. Для построения эллипса находим характерные точки большой и малой оси эллипса. Отмечаем точки a^/ b^/ c^/ d^/ , так как точки a^/ и c^/ лежат на очерковых образующих цилиндра, то они будут лежать на оси цилиндра на горизонтальной плоскости проекций. И, наоборот, точки b^/ и d^/ лежат на оси цилиндра на фронтальной плоскости проекций, тогда на горизонтальной плоскости проекций они будут лежать на очерковых образующих цилиндра. Полученные точки a, b, c, d соединяем плавной линией. С левой стороны достраиваем аналогично.

2. Отмечаем характерные точки пересечения очерковых образующих конуса и цилиндра – 1^/ ,2^/,3^/, 4^/.

3. Остальные точки на фронтальной плоскости проекций находим с помощью проекций вспомогательных сфер строим окружности из центра пересечения осей конуса и цилиндра-е^/. Например: берем радиус р1 и строим окружность, отмечаем точки пересечения данной окружности с образующими конуса (точки х-х) и пересечение с образующими цилиндра (точки у-у), полученные точки соединяем прямыми линиями и отмечаем точки пересечения этих прямых между собой (т.е. при пересечении х-х и у-у отмечаем точку 5^/ ,12^/ и 10^/). Остальные вспомогательные сферы (окружности) выбираем произвольно, главное чтобы они не выходили за самую крайнюю характерную точку (в данном случае это точка 1^/).

4. Самая минимальная окружность должна быть вписана или в цилиндр или в конус. В данном примере эта окружность вписана в цилиндр, следовательно, в цилиндре будет выстроена только одна вспомогательная линия у-у, а, соответственно, общих точек пересечения только две (6^/ и11^/).

5. Ближние точки соединяем между собой, получаем две кривые 2^/-6^/-5^/-3^/ и 1^/-7^/-8^/-9^/-10^/-11^/-12^/-13^/-4^/. В данном примере линии идут близко к образующим цилиндра, в других вариантах они могут идти близко к образующим конуса.

6. Находим точки на горизонтальной плоскости проекций. Сначала можем найти характерные точки 1,2,3, 4. Эти точки будут лежать на горизонтальной оси основания конуса, т.к. на фронтальной плоскости проекций они лежат на очерковых образующих конуса.

7. Все остальные точки находим с помощью вспомогательных окружностей. Каждая точка находится на вспомогательной линии х-х, принадлежащей конусу (эти линии получены при построении проекций сфер). Так как линии проходят параллельно основанию конуса, то в сечениях получаются окружности, радиусы которых измеряются от оси конуса до очерковой образующей (см. радиус r₁ для точки 5^/). Вспомогательные окружности строим на горизонтальной плоскости проекций из точки О. Затем на данную окружность сбрасываем точки.

8. Дальше определяем видимость кривой пересечения. Смотрим сверху: боковая поверхность конуса будет видна полностью, а боковая поверхность цилиндра будет видимой до оси цилиндра и невидимой под осью цилиндра. Так как кривая 1^/-7^/-8^/-9^/-10^/-11^/-12^/-13^/-4^/ на фронтальной плоскости проекций пересекает ось цилиндра в точках t₁^/ _и t₂^/ , то на горизонтальной плоскости проекций часть кривой t₁-11- t₂ будет видимой (она проходит над осью цилиндра). Остальная часть кривой будет невидимой, так как на фронтальной плоскости остальные точки расположены под осью цилиндра. Линия 2-6-5-3-5-6-2 будет видимой, так как на фронтальной плоскости проекций эти точки расположены над осью цилиндра. Остается показать невидимой линией часть основания конуса расположенного под проекцией цилиндра.

Задача №11.

Построить аксонометрическую проекцию прямого кругового конуса и трехгранной призмы. Показать линию (линии) их взаимного пересечения. Данные для своего варианта взять из условия задачи №7.

Указания к решению задачи №11.

Для решения задачи предварительно наносят оси координат в системе прямоугольной изометрии. По заданным координатам, взятым из таблицы 5, строят аксонометрические проекции конуса и призмы. При этом нужно построить вторичную проекцию призмы на плоскости ХОZ. Основание конуса находится на плоскости ХОY. Вторичную проекцию призмы (на плоскости ХОZ)строят тонкими линиями. Линию пересечения призмы и конуса удобно строить при помощи вспомогательных плоскостей, проходящих через вершину конуса и расположенных перпендикулярно плоскости ХОZ. В этом случае эти вспомогательные плоскости пересекают конус по образующим, которые легко находятся, а призма по прямым, параллельным боковым ребрам. На пересечении этих линий находят точки, которые и определяют линии пересечения конуса и призмы. Следует обратить внимание на определение точек, определяющих видимость линий пересечения.

Задача 11. Принцип решения:

1. Строим оси координат в аксонометрии. На плоскости ХОZ по заданным координатам строим проекции конуса и призмы. Точки определяем с помощью проекций вспомогательных образующих, проводя их из вершины конуса s^/ до основания.

2. По координатам Х и Y точки О, строят центр конуса, оси основания конуса располагаются параллельно осям координат. Из точки О поднимают ось конуса параллельно оси ОZ на высоту конуса. На плоскости ХОY строим основание конуса в виде эллипса. Из точки S проводим касательные к основанию, отмечаем точки касания и переносим их на проекцию конуса. Построенная образующая, пересечет проекцию призмы в точках 6^/ и 2^/. Правая образующая не пересекает проекцию призмы, следовательно, ее можно не показывать. Для точности построения линии пересечения грань b^/-c^/ разбивают вспомогательной точкой 4^/ произвольно, и проводят образующую из точки s^/ через точку 4^/ до основания конуса.

3. Последовательно переносим точки с проекции основания на эллипс и соединяем их с вершиной конуса (точки надо переносить параллельно оси ОY). Затем также параллельно оси ОY переносим точки на соответствующие образующие.

4. Полученные точки соединяем между собой в той же последовательности как на проекции призмы, т.е. 1-2-3-b-4-c-5-6-7.

5. Определяем видимость линии пересечения. Так как грань А-В видимая, то и точки на ней будут видимыми. Но необходимо учитывать границу видимости конуса- это образующая с точкой 2 слева. Остальная часть линии пересечения будет невидимой.

6. Достраиваем проекцию призмы. Из точек a^/ ,b^/ и c^/ проводим линии параллельно оси ОY. “Отставляем” призму от стены на то же расстояние, как показано на горизонтальной плоскости проекций в задаче 7 (расстояние от оси ох до основания призмы), полученные точки соединяем между собой, а затем откладываем длину призмы и достраиваем второе основание призмы. Показываем видимость призмы.

Пример работы показан в задаче 7. Обе задачи располагаем на одном листе.