Способы задания множеств
1. Перечислением своих элементов.
A={a,b,c,...}.
2. Через описание ограничительного свойства.
A={x| P(x)} - A множество таких элементов x, которые обладают свойством P(x).
В дальнейшем мы будем пользоваться общепринятыми обозначениями множеств:
N - множество натуральных чисел,
Z - множество целых чисел,
Q - множество рациональных чисел,
C - множество комплексных чисел,
R - множество действительных чисел,
 - пустое множество.
- пустое множество.
Подмножества. Универсальное множество. Множество всех подмножеств данного множества.
Понятие подмножества возникает тогда, когда необходимо рассматривать некоторое множество не самостоятельно, а как часть другого, более широкого множества.
Множество B называется подмножествоммножества A, если всякий элемент множества B является элементом множества A. Запись B A ( не исключает, что B=A).
A ( не исключает, что B=A).
Определённое ранее пустое множество по определению является подмножеством любого множества.
По определению пустое множество является конечным.
По определению множество является подмножеством самого себя, A A.
A.
Таким образом, у каждого множества (кроме пустого) есть по крайней мере два подмножества - само множество и пустое.
Истинным, строгим или собственным подмножеством множества А называется такое его подмножество В, что В А и В
А и В 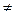 А. Запись В
А. Запись В 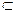 А, где
А, где 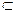 - знак строгого включения.
- знак строгого включения.
По отношению к множеству А - пустое множество и само множество А называется несобственным, нестрогим или не истинным подмножествами множества А.
Таким образом, мы имеем следующие свойства множеств:
1. А 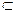 В
В  А
А В и А
В и А 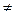 В.
В.
2. А В
В  А
А 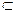 В или А=В.
В или А=В.
3. А 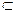 В
В А
А В.
В.
4. А 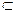 В
В  А
А 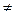 В.
В.
5. А В и В
В и В С
С  А
А С.
С.
6. А 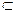 В и В
В и В 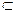 С
С А
А 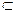 С.
С.
7. А В и В
В и В 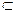 С
С А
А 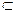 С.
С.
Первые четыре свойства следуют из введенных ранее определений.
Покажем выполнение остальных свойств.
Свойство 5.
Докажем его методом от противного.
Пусть А В и В
В и В С но А
С но А  С и А
С и А 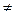 С.
С.
Тогда существует такой элемент а  А, но а
А, но а 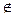 С. Тогда, т.к. В
С. Тогда, т.к. В С, то а
С, то а 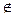 В.
В.
Получили противоречие: а  А, а
А, а 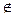 В, но А
В, но А В.
В.
Свойство 6.
Так как А 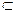 В и В
В и В 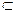 С, то по свойству 3 А
С, то по свойству 3 А В и В
В и В С и по свойству 5 А
С и по свойству 5 А С. Осталось показать, что А
С. Осталось показать, что А 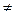 С. Пусть это не так и А=С . Т.е. для любого элемента а, а
С. Пусть это не так и А=С . Т.е. для любого элемента а, а  А
А  а
а  С. Так как В
С. Так как В 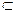 С, то В
С, то В 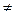 С и найдется элемент в,в
С и найдется элемент в,в 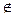 В. , но в
В. , но в  С. Так как А
С. Так как А 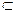 В, то в
В, то в 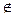 А. Отсюда элемент в присутствует в множестве С, но отсутствует в множестве А, отсюда эти множества не равны.
А. Отсюда элемент в присутствует в множестве С, но отсутствует в множестве А, отсюда эти множества не равны.
Свойство 7.
Так как В 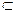 С, то по свойству 3 В
С, то по свойству 3 В С и тогда по свойству 5 А
С и тогда по свойству 5 А С. Осталось показать, что А
С. Осталось показать, что А 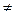 С. Действительно, так как В
С. Действительно, так как В 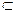 С, то найдется элемент а, а
С, то найдется элемент а, а  С, но а
С, но а 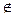 В. Так как А
В. Так как А В, то а
В, то а 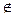 А. Отсюда а
А. Отсюда а  С, но а
С, но а 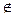 А, т.е. А
А, т.е. А 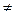 С.
С.
Если все рассматриваемые в ходе рассуждений множества являются подмножествами некоторого фиксированного множество J, то это множество называют универсальным( для рассматриваемого набора множеств)множеством или универсом.Таким образом, универс - это такое множество,что любоерассматриваемое множество является его подмножеством.
Рассмотрим множество А={a,b,c}. Найдем все его различные подмножества. Это: пустое множество  , три одноэлементных подмножества {a}, {b}, {c}, три двухэлементных подмножества {a,b}, {a,c}, {b,c} и одно трёхэлементное множества - само множество А. Множество всех подмножеств множества А будем обозначать как P(A) или
, три одноэлементных подмножества {a}, {b}, {c}, три двухэлементных подмножества {a,b}, {a,c}, {b,c} и одно трёхэлементное множества - само множество А. Множество всех подмножеств множества А будем обозначать как P(A) или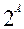 .
.
