Тема 1. Элементы линейной алгебры

МАТЕМАТИКА

Методические указания к изучению курса

и контрольные задания для студентов

заочной формы обучения направлений

151900 «Конструкторско-технологическое обеспечение машиностроительных производств» и 150700 «Машиностроение»

(I семестр)

Брянск 2012

УДК 511

Математика [Текст]+[Электронный ресурс]: методические указания к изучению курса и контрольные задания для студентов заочной формы обучения направлений 151900 «Конструкторско-технологическое обеспечение машиностроительных производств» и 150700 «Машиностроение» (I семестр). – Брянск: БГТУ, 2012. – 40 с.

Разработали: Е.С. Золотухина, канд. физ.-мат. наук, доц.;

А.И. Горелёнков, канд. техн. наук, доц.

Рекомендовано кафедрой «Высшая математика» БГТУ

(протокол №5 от 31.01.12)

Научный редактор В.М. Кобзев

Редактор издательства Т.И. Королева

Компьютерный набор Е.С. Золотухина

Темплан 2012 г., п. 159

Подписано в печать 18.06.12 Формат 60х84 1/16 Бумага офсетная

Офсетная печать. Печ. л. 2,32 Уч.-изд. л. 2,32 Т. 30 экз. Заказ

Издательство Брянского государственного технического университета

Брянск, бульвар 50-летия Октября, 7

Лаборатория оперативной печати БГТУ, ул. Институтская, 16.

ПРЕДИСЛОВИЕ

Настоящие МУ предназначены для оказания помощи студентам при изучении дисциплины «Математика» в первом семестре. Они содержат список рекомендуемой литературы, методические рекомендации к изучению тем курса и выполнению контрольных работ и задачи для контрольных работ.

В соответствии с рабочей программой дисциплины в первом семестре студенты изучают темы «Элементы линейной алгебры», «Элементы векторной алгебры», «Аналитическая геометрия на плоскости», «Аналитическая геометрия в пространстве», «Введение в математический анализ». Каждая тема состоит из нескольких разделов. В конце раздела в квадратных скобках указаны ссылки на пособия из приведенного списка литературы. После изучения определенной темы необходимо рассмотреть примеры решения задач.

По дисциплине «Математика» студенты в первом семестре сдают экзамен после выполнения предусмотренных учебным планом двух контрольных работ. Задания к ним приводятся в данных указаниях. При выполнении работ и их оформлении следует придерживаться следующих правил:

– студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой номера его зачетной книжки.

– работа должна быть выполнена в тетради, имеющей поля для замечаний рецензента;

– перед решением каждой задачи нужно привести полностью ее условие;

– следует придерживаться той последовательности при решении задач, в какой они даны в задании;

– на обложке тетради указываются наименование учебной дисциплины, номер контрольной работы, фамилия, имя, отчество (полностью) студента, номер его группы и зачетной книжки, фамилия, имя, отчество рецензента.

Список рекомендуемой литературы

1. Ильин, В.А., Ким, Г.Д. Линейная алгебра и аналитическая геометрия / В.А. Ильин, Г.Д. Ким. – М.: ТК Велби, Изд-во Проспект, 2007. – 400 с.

2. Беклемишев, Д.В. Курс аналитической геометрии и линейной алгебры /Д.В. Беклемишев. – М.: Физматлит, 2001. – 376 с.

3. Бугров, Я.С., Никольский, С.М. Высшая математика / Я.С. Бугров, С.М. Никольский. Т.1. Элементы линейной алгебры и аналитической геометрии. – М.: Дрофа, 2003.– 288 с.

4. Данко, П.Е., Попов, А.Г., Кожевникова, Т.Я. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высш. шк., 1999. – Ч. 1. – 304 с.

5. Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. − 2-е изд., испр. − М.: Айрис-пресс, 2002. – Ч. 1. − 288 с.

6. Ефимов, Н.В. Краткий курс аналитической геометрии / Н.В. Ефимов. – М.: Физматлит, 2002. – 240 с.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ИЗУЧЕНИЮ ТЕМ КУРСА И ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

Тема 1. Элементы линейной алгебры

Матрицы. Действия над матрицами. [3, §1]. Определители. Свойства определителей. [3, §2]. Невырожденные матрицы. Обратная матрица. [3, §3]. Ранг матрицы. [3, §3]. Системы линейных алгебраических уравнений. Решение систем линейных алгебраических уравнений по правилу Крамера, с помощью обратной матрицы, методом Гаусса. [3, §4].

Пример 1. Дана матрица 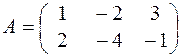. Найти .

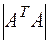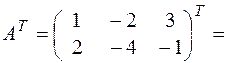
Решение: Транспонируем матрицу :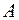
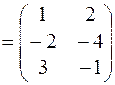. Матрица 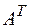имеет размерность 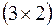, матрица 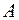имеет размерность 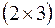. Значит, произведение этих матриц возможно, и матрица 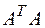будет иметь размерность .

.

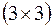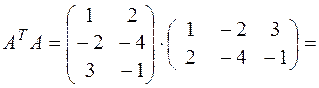
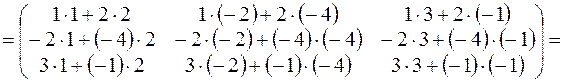
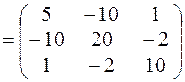Определитель матрицы 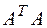найдем, воспользовавшись «правилом треугольников»:

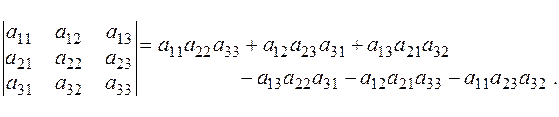
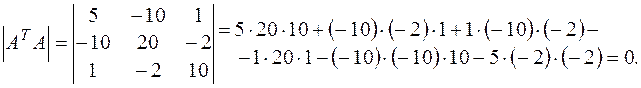
Пример 2. Решить систему уравнений 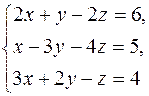1) по правилу Крамера; 2) с помощью обратной матрицы; 3) методом Гаусса.

Решение: 1. Найдем главный определитель системы:

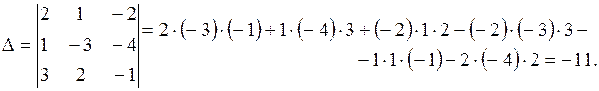
Так как 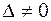, то система имеет единственное решение.

Найдем вспомогательные определители системы:

; ; .

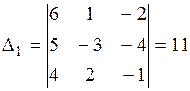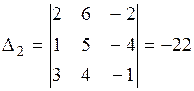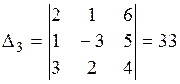Значит, ; ; .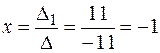

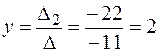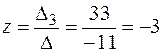2. Запишем заданную систему уравнений в матричной форм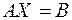е , где 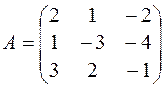– матрица коэффициентов системы; 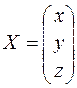– столбец неизвестных; 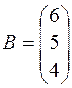– столбец свободных членов.

Тогда 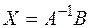, где 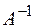– обратная матрица к матрице .

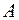Так как 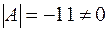, то 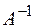существует. Обратная матрица 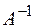может быть найдена по формул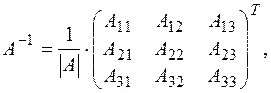е где 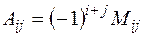– алгебраическое дополнение элемента 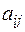матрицы 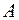; 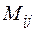– минор элемента 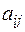матрицы 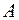, то есть определитель, полученный из матрицы 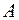путем вычеркивания 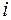-й строки и 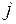-го столбца.

Определитель второго порядка может быть найден по формуле .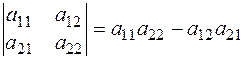

Находим алгебраические дополнения элементов матрицы :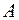

;
; .

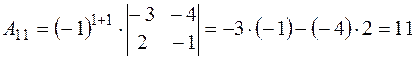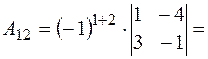
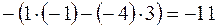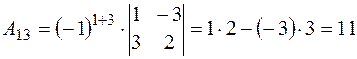Аналогично ; ; ; ; ; .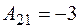

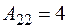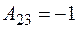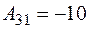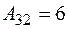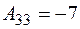Значит, .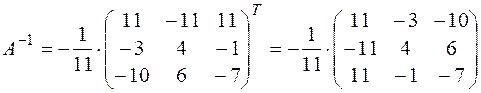

Тогда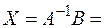

,

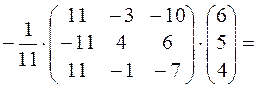
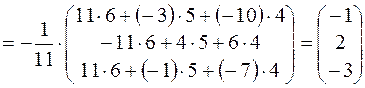то есть , , .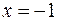

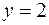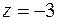3. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду:

.

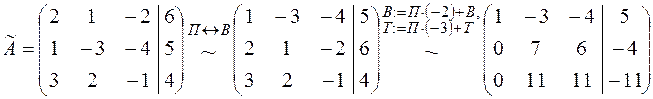
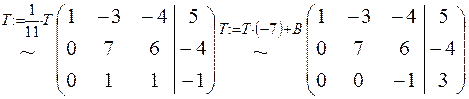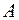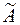Откуда следует, что ранги матриц и равны 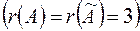, то есть система уравнений совместна. Число неизвестных 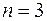, значит, система уравнений имеет единственное решение.

Перейдем от полученной ступенчатой матрицы к системе, эквивалентной заданной: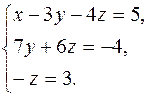

Решая систему «снизу вверх», получаем, что 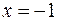, , .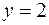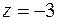