Тригонометрический ряд. Ряд Фурье
Кафедра МИС и ПО
МАТЕМАТИКА
Методические рекомендации
По выполнению контрольной работы по теме
«Ряды Фурье»
Для студентов 2-3 курсов вечерне-заочного факультета
Мурманск
2015 г.
Составитель – Хохлова Людмила Ивановна, доцент кафедры МИС и ПО МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой
_______________ 2015 г., протокол №
Рецензент – Р. А. Богомолов, канд. физ.-мат. наук, доцент кафедры МИС и ПО МГТУ
ÓМурманский государственный технический университет, 2015
Оглавление
Введение. 5
§1. Тригонометрический ряд. Ряд Фурье. 7
§2. Ряд Фурье для четных и нечетных функций. 12
§3. Ряды Фурье для функций произвольного периода. 14
§4. Разложение в ряд Фурье непериодической функции. 15
§5. Задача о разложении в ряд Фурье функции, заданной на отрезке [0, π] ([0.l]) по синусам или по косинусам. 18
§6. Комплексная форма ряда Фурье. 22
§7. Амплитудно-частотный спектр ряда Фурье. 24
§8. Использование методов численного интегрирования при разложении функции в ряд Фурье. 26
Варианты контрольной работы по теме «Ряды Фурье». 40
Требования к оформлению контрольных работ
1. Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса, используя учебники и справочный материал, приведенный в конце данного текста.
2. Выполнять контрольную работу следует в отдельной тетради, либо в отпечатанном виде (формат А4) со скрепленными и пронумерованными листами. Не допускается выполнение работы карандашом.
3. На обложке тетради (титульном листе отпечатанного варианта) должны присутствовать:
название дисциплины;
фамилия, имя, отчество студента (полностью);
шифр специальности и студента, курс;
номер варианта;
дата отправки работы в университет.
4. Решения задач необходимо выполнять в той же последовательности, что и в условиях задач. Решение каждой задачи следует начинать с новой страницы, оставляя поля и места для замечаний преподавателя-рецензента.
5. В начале решения каждой задачи следует записать ее условие и перечислить исходные данные выбранного варианта. В конце решения должен быть ответ, выделенный отдельной строкой.
6. При использовании формул в решении следует сначала выписать теоретическую формулу, пояснив значение и смысл каждого обозначения.
7. Все графики и чертежи выполняются крупно, с пояснениями: на осях координат следует указывать обозначение каждой оси и масштаб; все используемые точки, линии и векторы должны быть подписаны.
8. Ответ в каждой задаче следует писать либо в виде точного десятичного числа, либо в виде приближенного десятичного числа, сохраняя в нем два знака после запятой. При решении задачи все промежуточные приближенные результаты следует писать, сохраняя в них три-четыре знака после запятой.
Введение
В настоящем пособии содержатся методические рекомендации к изучению теоретического материала и выполнению контрольной работы по теме «Ряды Фурье», варианты этой контрольной работы, примерный вариант и его решение, список рекомендуемой литературы.
В результате изучения темы «Ряды Фурье» студенты должны научиться строить:
1. Ряд Фурье для функций с периодом 2π .
2. Ряды Фурье для функций произвольного периода.
3. Ряд Фурье для четных и нечетных функций.
4. Ряд Фурье непериодической функции.
5. Ряд Фурье функции, заданной на отрезке [0, π] по синусам или по косинусам
6. Ряд Фурье в комплексной форме
7. Амплитудно-частотный спектр ряда Фурье
8. Использовать методы численного интегрирования при разложении функции в ряд Фурье
Данные методические рекомендации включают также справочный материал, необходимый для выполнения контрольной работы по теме «Ряды Фурье», и подробное решение примерного варианта работы.
| № | Тема | Литература |
| Гармонические колебания. Тригонометрический ряд. Ряд Фурье. | [1], гл.VII, §29, 30; [2], гл.7, §1-4; [3], ч.1, гл.IX, №1337-1349, 1368-1379, 1392-1396; [4], гл.6, № 2-12, 36-50, 102, 108, 114, 118 | |
| Ряд Фурье для функций с произвольным периодом | [1], гл.VII, §31, 32; [2], гл.7, §5, 6.3; [3], ч.1, гл.IX, №1410-1414, 1429-1434, 1489-1490, 1493-1499; [4], гл.6, № 174, 177-180, 193, 195-201, 230-240 | |
| Ряд Фурье для четных и нечетных функций | [1], гл.VIII, §35-40; [2], гл.8, §1, 4-9, 11; [3], ч.1, гл.X, №1552-1557, 1572-1578; [4], гл.6, № 262-273, 255-260, 366-369 | |
| Ряд Фурье функции, заданной на отрезке [0, π] по синусам или по косинусам | [1], гл. VIII, §41, 41.1, 41.2; [2], гл.8, §10.1, 10.2; [3], ч.1, гл.X, №1596-1600; [4], гл.6, № 290-294,301, 302 | |
| Ряд Фурье в комплексной форме | [1], гл. VIII, §41.4; [2], гл.8, §10.4; [3], ч.1, гл.X, №1628-1631; [4], гл.6, № 319-323 | |
| Использование методов численного интегрирования при разложении функции в ряд Фурье | [1], гл. VIII, §41.3; [2], гл.8, §10.3; [3], ч.1, гл.X, №1613-1615; [4], гл.6, № 307-310, 312 |
Примечание. Ссылки на литературу в таблице, даны в соответствии с номерами в списке рекомендуемой литературы.
Тригонометрический ряд. Ряд Фурье.
В науке и технике часто приходится иметь дело с периодическими явлениями, т.е. такими, которые воспроизводятся через определённый промежуток времени T, называемый периодом. Простейшей из периодических функций (если не считать постоянной) является синусоидальная величина: Asin( 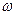 x+
x+ 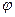 ), гармоническое колебание, где
), гармоническое колебание, где 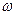 есть «частота», связанная с периодом соотношением:
есть «частота», связанная с периодом соотношением: 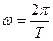 . Из таких простейших периодических функций могут быть составлены более сложные. Очевидно, что составляющие синусоидальные величины должны быть разных частот, так как сложение синусоидальных величин одной и той же частоты приводит к синусоидальной величине той же частоты. Если сложить несколько величин вида
. Из таких простейших периодических функций могут быть составлены более сложные. Очевидно, что составляющие синусоидальные величины должны быть разных частот, так как сложение синусоидальных величин одной и той же частоты приводит к синусоидальной величине той же частоты. Если сложить несколько величин вида
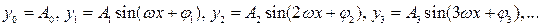 ,
,
которые, если не считать постоянной, имеют частоты 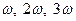 , кратные наименьшей из них,
, кратные наименьшей из них, 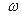 , и периоды
, и периоды 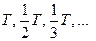 , то получится новая периодическая функция (с периодом T), отличная от этих величин.
, то получится новая периодическая функция (с периодом T), отличная от этих величин.
Для примера мы воспроизводим здесь сложение трех синусоидальных величин: 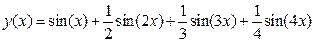 . Рассмотрим график этой функции
. Рассмотрим график этой функции
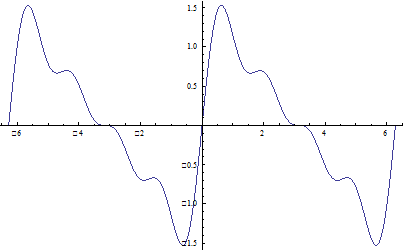
Этот график значительно отличается от синусоиды. Еще в большей степени это имеет место для суммы бесконечного ряда, составленного из слагаемых этого вида. Поставим вопрос: можно ли данную периодическую функцию периода Т представить в виде суммы конечного или хотя бы бесконечного множества синусоидальных величин? Оказывается, по отношению к большому классу функций на этот вопрос можно дать утвердительный ответ, но это только если привлечь именно всю бесконечную последовательность таких слагаемых. Геометрически это означает, что график периодической функции получается путем наложения ряда синусоид. Если же рассматривать каждую синусоидальную величину как некоторое гармоническое колебательное движение, то можно сказать, что это сложное колебание, характеризуемое функцией 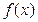 или просто ее гармониками (первой, второй и т. д.). Процесс разложения периодической функции на гармоники носит название гармонического анализа.
или просто ее гармониками (первой, второй и т. д.). Процесс разложения периодической функции на гармоники носит название гармонического анализа.
Важно отметить, что подобные разложения часто оказываются полезными и при исследовании функций, заданных лишь в определенном конечном промежутке и вовсе не порожденных никакими колебательными явлениями.
Определение. Тригонометрическим рядом называется ряд вида:
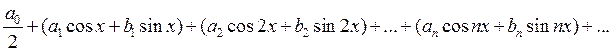 или
или 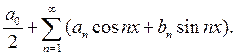 (1).
(1).
Действительные числа 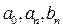 называются коэффициентами тригонометрического ряда. Этот ряд можно записать и так:
называются коэффициентами тригонометрического ряда. Этот ряд можно записать и так: 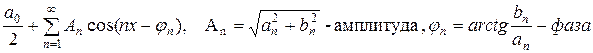
Если ряд представленного выше типа сходится, то его сумма является периодической функцией с периодом 2p.
Определение. Коэффициентами Фурье тригонометрического ряда называются: 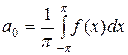 (2)
(2)
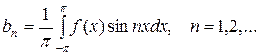 (3)
(3)
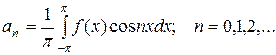 (4)
(4)
Определение. Рядом Фурье для функции f(x) называется тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье.
Если ряд Фурье функции f(x) сходится к ней во всех ее точках непрерывности, то говорят, что функция f(x) разлагается в ряд Фурье.
Теорема. (Теорема Дирихле) Если функция 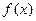 имеет период 2p и на отрезке
имеет период 2p и на отрезке 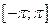 непрерывна или имеет конечное число точек разрыва первого рода, отрезок
непрерывна или имеет конечное число точек разрыва первого рода, отрезок 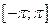 можно разбить на конечное число отрезков так, что внутри каждого из них функция
можно разбить на конечное число отрезков так, что внутри каждого из них функция 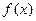 монотонна, то ряд Фурье для функции
монотонна, то ряд Фурье для функции 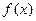 сходится при всех значениях х, причем в точках непрерывности функции
сходится при всех значениях х, причем в точках непрерывности функции 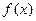 его сумма S(x) равна
его сумма S(x) равна 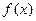 , а в точках разрыва его сумма равна
, а в точках разрыва его сумма равна 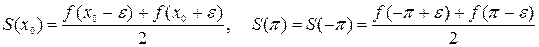 , т.е. среднему арифметическому предельных значений слева и справа.
, т.е. среднему арифметическому предельных значений слева и справа.
При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции 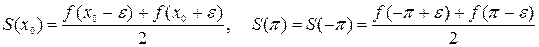 .
.
Функция, удовлетворяющая условиям этой теоремы, называется кусочно – гладкой на отрезке 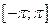 .
.
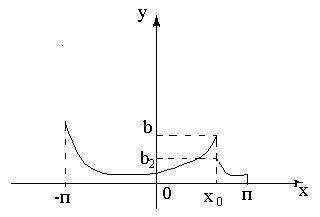
Рассмотрим примеры на разложение функции в ряд Фурье.
Пример 1. Разложить в ряд Фурье функцию f(x)=1-x, имеющую период 2p и заданную на отрезке 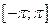 .
.
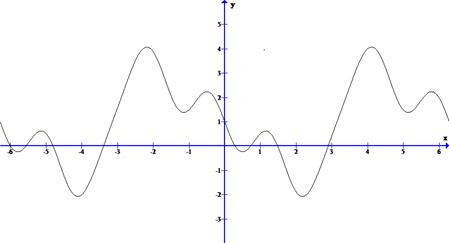
Решение. Построим график этой функции
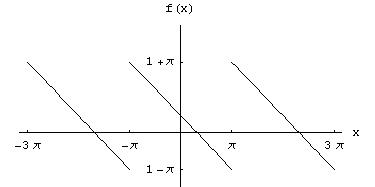
Эта функция непрерывна на отрезке 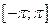 , то есть на отрезке длиной в период, поэтому допускает разложение в ряд Фурье, сходящейся к ней в каждой точке этого отрезка. По формуле (2) найдем коэффициент
, то есть на отрезке длиной в период, поэтому допускает разложение в ряд Фурье, сходящейся к ней в каждой точке этого отрезка. По формуле (2) найдем коэффициент 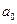 этого ряда:
этого ряда: 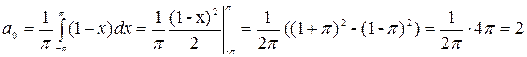 .
.
Применим формулу интегрирования по частям и найдем 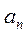 и
и 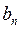 по формулам (3) и (4) соответственно:
по формулам (3) и (4) соответственно:
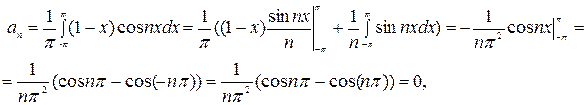
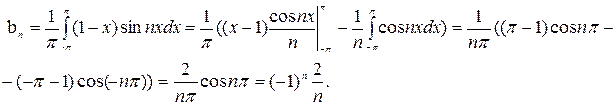 Подставляя коэффициенты в формулу (1), получаем
Подставляя коэффициенты в формулу (1), получаем 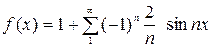 или
или 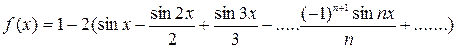 .
.
Это равенство имеет место во всех точках, кроме точек 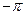 и
и 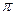 (точки склейки графиков). В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть
(точки склейки графиков). В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть 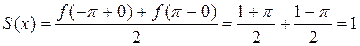 .
.
Приведем алгоритм разложения функции 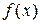 в ряд Фурье.
в ряд Фурье.
Общий порядок решения поставленной задачи сводится к следующему:
1. построение графика заданной функции 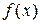 и проверка выполнения условий Дирихле;
и проверка выполнения условий Дирихле;
2. вычисление коэффициентов 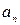 и
и 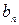 по формулам (2-4);
по формулам (2-4);
3. составление ряда Фурье заданной функции f(x) в точках ее непрерывности: 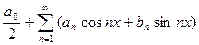 ;
;
4. определение точек разрыва функции f(x);
5. нахождение среднего арифметического предельных значений функции f(x) справа и слева в точке разрыва 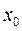 и на концах отрезка
и на концах отрезка 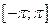 , если
, если 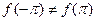 . В этом случае
. В этом случае 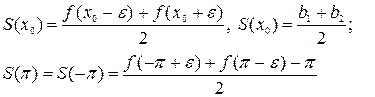
Замечание. При вычислении коэффициентов Фурье мы можем заменять промежуток интегрирования 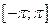 промежутком интегрирования
промежутком интегрирования 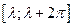 , где l - любое действительное число, а
, где l - любое действительное число, а 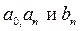 вычислять по формулам:
вычислять по формулам: 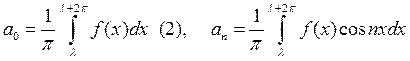 ,
, 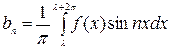 .
.
Вопросы для самопроверки
1. Дайте определение гармонического колебания
2. Дайте определение ряда Фурье
3. Запишите коэффициенты ряда Фурье
4. Сформулируйте теорему Дирихле
