Алгебраические фракталы

Авторы: Вовк С.К.

Ивашко А.С.

10 класс, МОУ МГМЛ

Научный руководитель:

Квасова Н.А., старший преподаватель кафедры математики МГТУ

Магнитогорск

2012г.

Фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба.

История

Слова «фрактал» и «фрактальность» появились в научной литературе сравнительно недавно и еще не успели войти в большинство словарей, справочников и энциклопедий. Слово «фрактал» образовано от латинского «fractus», что в переводе означает «состоящий из фрагментов». Придумал его в 1975 году математик Бенуа Мандельброт, который сумел открыть рядом с нами поистине удивительный мир, по-новому взглянув на многие, казалось бы, хорошо знакомые предметы и явления. В своих исследованиях Мандельброт обратил внимание на то, что при всей своей очевидности ускользало от его предшественников: контуры, поверхности и объемы окружающих нас предметов не так ровны, гладки и совершенны, как принято думать. В действительности они пронизаны трещинами и порами, покрыты сетью морщин, царапин и отверстий самой причудливой формы. Вы, к примеру, видели узоры на стекле после мороза или хитроумные кляксы, оставленные на листе чернильной ручкой, так вот что-то подобное вполне можно записать в виде некоторого алгоритма. Подобные множества называю фрактальными. Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию обо всем фрактале. Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком- то смысле подобны целому». Чтобы представить себе фрактал более наглядно рассмотрим ставший классическим пример: «Какова длина берега Британии?». Ответ на этот вопрос не так прост, как кажется. Все зависит от длины инструмента, которым мы будем пользоваться. Измерив берег с помощью километровой линейки, мы получим какую-то длину. Однако мы пропустим множество небольших заливов и полуостровов, которые по размеру намного меньше нашей линейки. Уменьшив размер линейки до одного метра, мы учтем эти детали ландшафта, и, соответственно длина берега станет больше. Пойдем дальше и, измерив длину берега с помощью миллиметровой линейки, обнаружим, что она будет еще больше. В итоге ответ на такой, казалось бы, простой вопрос («Какова длина берега Британии?») может поставить в тупик кого угодно: длина берега Британии бесконечна.

Как определить фрактал:

- обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.

Фрактал - является самоподобной или приближённо самоподобной.

Классификации фракталов

В основном фракталы делят на геометрические, алгебраические и стохастические.

Геометрические фракталы

Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется начальный набор отрезков, на основании которых будет строиться фрактал. Далее к этому набору применяют правила, которые преобразует его в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем бесконечное количество преобразований - получим геометрический фрактал.

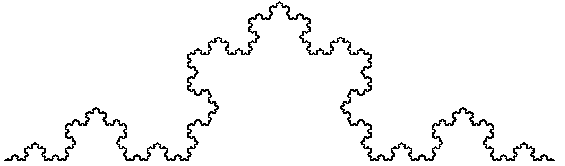
Снежинка Коха

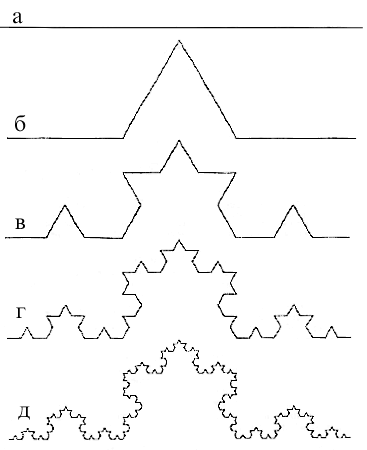
Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д…

Алгебраические фракталы

Множество Мандельброта - один из самых известных фрактальных объектов. Отрытое в 1976 году Бенуа Мандельбротом, это удивительное множество стало наиболее знаменитым фрактальным объектом, несущим в себе неисчерпаемое число самоподобных деталей.

При создании множества Мандельброта используется алгебраическое выражение

Z_n+1=Z_n²+C,(1) где Z и C – комплексные числа, а Z0=0.

Комплексное число имеет две части: действительную Х (Re) и мнимую У (Im). Разделим выражение (1) на действительную и мнимую части:

X_i+1=X_i²-Y_i²+a

Y_i+1=2*X_i*Y_i+b (2)

Для каждой точки (a,b) проводится серия вычислений по формулам (2), причем Х0 и У0 принимаются равными нулю. Результат вычислений изображается графически на комплексной плоскости в системе координат OХУ, где ось Х предназначена для действительных величин, ось У - для мнимых. Полное изображение множества Мандельброта строится на участке координатной плоскости от -2 до 1 по оси Х, и от -1,5 до 1,5 - по оси У.

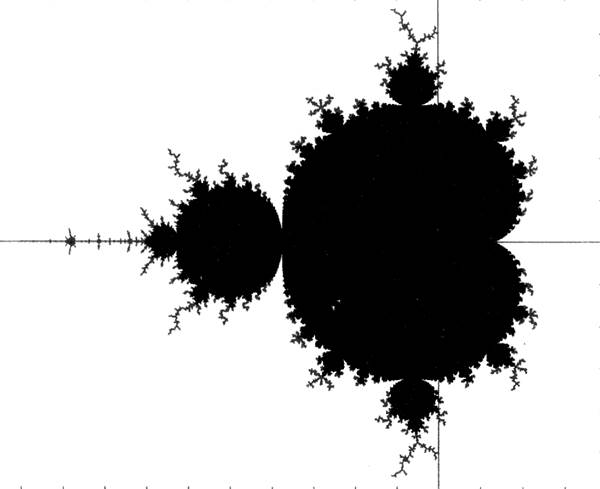
Визуально, внутри множества Мандельброта можно выделить бесконечное количество элементарных фигур, причём самая большая в центре представляет собой кардиоиду. Также есть набор овалов, касающихся кардиоиды, размер которых постепенно уменьшается, стремясь к нулю. Каждый из этих овалов имеет свой набор меньших овалов, диаметр которых также стремится к нулю и т. д. Этот процесс продолжается бесконечно, образуя фрактал. Также важно, что эти процессы ветвления фигур не исчерпывают полностью множество Мандельброта: если рассмотреть с увеличением дополнительные «ветки», то в них можно увидеть свои кардиоиды и круги, не связанные с главной фигурой. Самая большая фигура (видимая при рассматривании основного множества) из них находится в области от −1,78 до −1,75 на отрицательной оси действительных значений.