Исследование функции при помощи производных
Теоремы о среднем
При исследовании поведения дифференцируемых на некотором отрезке [a,b] функций важны следующие теоремы о среднем.
Теорема (Ролль). Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка с, a < с < b, в которой производная f¢(x) равная нулю, т.е. f¢(с) = 0.
Доказательство. По свойству функций, непрерывных на отрезке функция f(x) на отрезке [a, b] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M ¹ m.
Пусть M = m. Тогда функция f(x) на отрезке [a, b] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае в качестве с можно принять любую точку интервала.
Пусть М ≠ m. Так как значения на концах отрезка равны, то функция принимает хотя бы одно из значений М или m во внутренней точке с интервала (a,b). Пусть, например, функция принимает значение М в точке х = с (a < с < b), т.е. f(с) = M. Так как М - наибольшее значение функции, то для всех 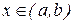 выполняется неравенство
выполняется неравенство 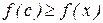 .
.
Найдём производную f¢(x) в точке х = с:

В силу предыдущего неравенства выполняется условие 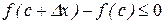 , если
, если  , т.е.
, т.е. 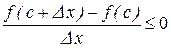 и поэтому
и поэтому  .
.
Если же 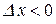 , т.е.
, т.е. 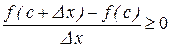 , то
, то 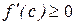 .
.
Таким образом, 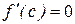
В случае, когда f(с) = m, доказательство аналогичное.
Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует по крайней мере одна точка с, в которой касательная к графику y = f(x) параллельна оси Ох.
Теорема (Коши). Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g¢(x) ¹ 0 на интервале (a, b), то существует по крайней мере одна точка с, a < с < b, такая, что
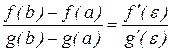 .
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке с.
Доказательство. Рассмотрим вспомогательную функцию
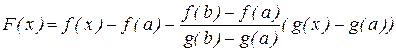 ,
,
которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка с, a < с < b, такая, что F¢(с) = 0. Т.к.
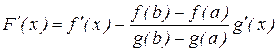 , то
, то
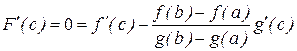
Но 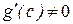 , то
, то 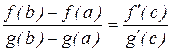 . Теорема доказана.
. Теорема доказана.
Теорема (Лагранж). Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка с 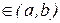 , такая, что выполняется равенство
, такая, что выполняется равенство
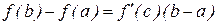 . (5.13)
. (5.13)
Доказательство. Теорему Лагранжа можно рассматривать, как частный случай теоремы Коши. Действительно, положим g(x) = х, тогда g¢(x)=1, g¢(с)=1 и 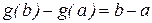 . Подставляя эти значения в формулу
. Подставляя эти значения в формулу
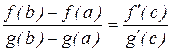 получаем
получаем 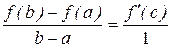 или
или
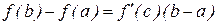 . Теорема доказана.
. Теорема доказана.
Полученное выражение (5.13) называется формулой Лагранжа или формулой конечных приращений. Согласно этой формуле приращение дифференцируемой функции на отрезке [a, b] равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.
Раскрытие неопределённостей(правила Лопиталя)
К разряду неопределенностей, связанных с вычислением пределов, принято относить следующие соотношения:
 .
.
Теорема (правило Лопиталя) Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х® а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.
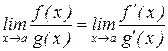 .
.
Доказательство. Применив формулу Коши, получим:
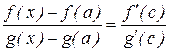
где с - точка, находящаяся между а и х. Учитывая, что f(a) = g(a) = 0:
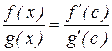
Пусть при х ® а отношение 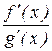 стремится к некоторому пределу. Т.к. точка с лежит между точками а и х, то при х ® а получим с ® а, а следовательно и отношение
стремится к некоторому пределу. Т.к. точка с лежит между точками а и х, то при х ® а получим с ® а, а следовательно и отношение 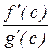 стремится к тому же пределу. Таким образом, можно записать:
стремится к тому же пределу. Таким образом, можно записать:
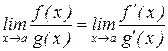 . Теорема доказана.
. Теорема доказана.
Примеры. 1) Найти предел: 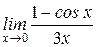 =
= 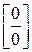 =
= 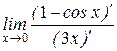 =
= 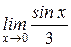 = 0
= 0
2) Найти предел: 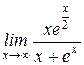 .
.
 ;
; 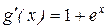 ;
;
 ;
; 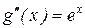 ;
;

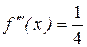 ;
; 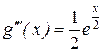 ;
; 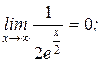
следует заметить, что правило Лопиталя – всего лишь один из способов вычисления пределов. Часто в конкретном примере наряду с правилом Лопиталя может быть использован и какой – либо другой метод (замена переменных, домножение и др.).
3) Найти предел: 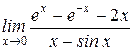 .
.
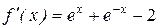 ;
; 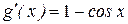 ;
;
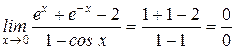 - опять получилась неопределенность.
- опять получилась неопределенность.
Применим правило Лопиталя еще раз.
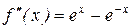 ;
; 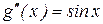 ;
;
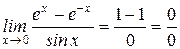 - применяем правило Лопиталя еще раз.
- применяем правило Лопиталя еще раз.
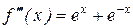 ;
; 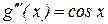 ;
;
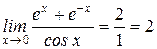 ;
;
Неопределенности вида 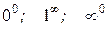 можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида
можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида 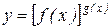 , f(x) > 0 вблизи точки а при х ® а. Для нахождения предела такой функции достаточно найти предел функции
, f(x) > 0 вблизи точки а при х ® а. Для нахождения предела такой функции достаточно найти предел функции
ln y = g(x) lnf(x).
4). Найти предел 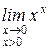 .
.
Здесь y = x x, ln y = x lnx.
Тогда 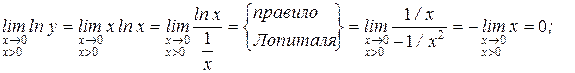 . Следовательно
. Следовательно 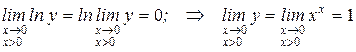
5) Найти предел 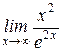 .
.
 ;
;  - получили неопределенность.
- получили неопределенность.
Применяем правило Лопиталя еще раз.
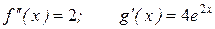 ;
; 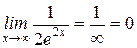 .
.
