Основная позиционная задача по построению точки пересечения прямой с плоскостью

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИИ

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

МИАССКИЙ ФИЛИАЛ

МАШИНОСТРОИТЕЛЬНЫЙ ФАКУЛЬТЕТ

КАФЕДРА ТЕХНИЧЕСКОЙ МЕХАНИКИ

Бережко Л.Н

МЕТОДИЧЕСКОЕ ПОСОБИЕ

Для студентов очной формы обучения

По выполнению задания №1

«Точка, прямая, плоскость»

(курс начертательной геометрии)

Миасс,2015

ВВЕДЕНИЕ

В данном задании задачи решаются с использованием метода замены плоскостей проекций (задачи «2 и 3) и без замены плоскостей проекций (задача №1). Суть метода замены плоскостей проекций и принципы решения задач этим методом подробно разобраны в методическом пособии «Решение метрических задач методом замены плоскостей проекций».

Целью данной работы является демонстрация простоты решения задачи №1 с использованием метода замены плоскостей проекций и без него. Следовательно, для успешного решения задания студенту необходимо освоить не только теоретическую часть темы «Точка. Прямая. Плоскость», но и сам метод замены плоскостей проекций.

Задача №1 Построение линии пересечения двух плоскостей

Подготовка исходных данных

Даны координаты точек А, В, С, К, L, M.

Построить проекции линии пересечения двух плоскостей треугольника АВС и параллелограмма KLMN, определить видимость плоскостей.

Точки в задаче заданы с помощью координат, а решение задачи проводится в ортогональных проекциях. Следовательно, чтобы приступить к решению задачи надо построить проекции точек по координатам, затем создать из них треугольник АВС и параллелограмм KLMN.

Для построения проекций точек надо знать взаимосвязь между проекциями точки и ее координатами.

Горизонтальная проекция точки определяется координатами X и Y.

Фронтальная проекция точки определяется координатами X и Z.

Например: точка А задана координатами (20, 5, 30),где X =20, Y=5, Z=30. Зададим оси координат X, Y, Z . Построим проекции точки А (рис.1).

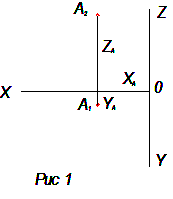
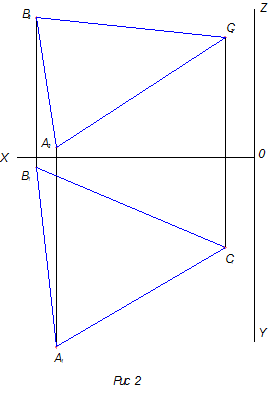
Так как в задании необходимо работать с плоскостями, то из точек создадим эти плоскости. Для этого необходимо соединить точки АВС, то есть на чертеже соединить одноименные проекции точек АВС и получить проекции треугольника АВС (рис.2).

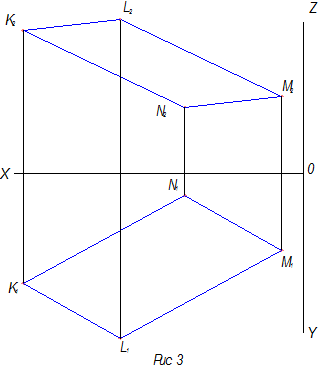
Для создания параллелограмма KLMN по трем точкам надо вспомнить свойство сторон параллелограмма, а именно: противоположные стороны параллелограмма равны и параллельны. Это свойство распространяется и на проекции параллелограмма: проекции противоположных сторон равны и параллельны.

На рисунке 3 проведены все эти построения.

Основная позиционная задача по построению точки пересечения прямой с плоскостью

Для решения задачи по построению линии пересечения плоскостей воспользуемся первой позиционной задачей по нахождению точки пересечения прямой и плоскости.

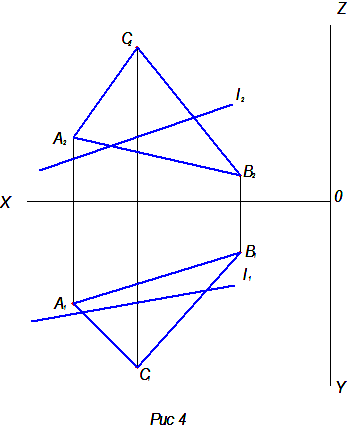
Пусть даны прямая и плоскость общего положения (см. рис. 4). Для того чтобы найти точку пересечения прямой с плоскостью надо:

1.через прямую провести проецирующую плоскость,

2.построить линию пересечения заданной плоскости с проецирующей,

3.найти точку пересечения заданной прямой с построенной линией пересечения плоскостей. Это и есть точка пересечения прямой с плоскостью.

Разберем решение этой задачи по частям.

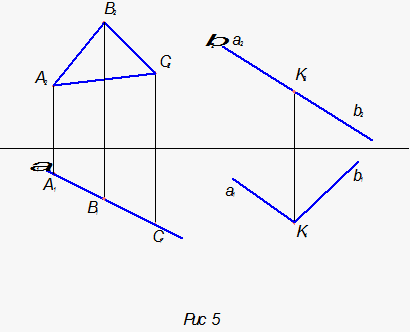
1) Через прямую провести проецирующую плоскость – это значит, что прямая лежит в проецирующей плоскости. В свою очередь проецирующая плоскость – это плоскость, которая на одну из плоскостей проекций проецируется в прямую ( см. рис.5 ).Если прямая лежит в этой плоскости, то она также будет проецироваться в эту прямую. Это значит, что для того чтобы на чертеже через прямую провести проецирующую плоскость, надо выполнить запись : проекция прямой совпадает с проекцией плоскости ( см. рис.6 ).

.

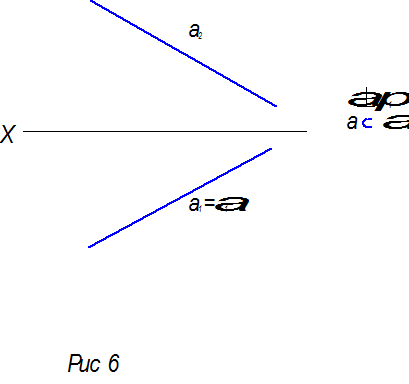
2) Линией пересечения двух плоскостей есть прямая, которая принадлежит обеим плоскостям. Так как одна плоскость проецирующая, то проекция этой прямой совпадет с проекцией проецирующей плоскости, то есть с прямой, в которую проецируется плоскость.

Недостающая проекция прямой находится из условия принадлежности прямой плоскости общего положения (см. рис.7).

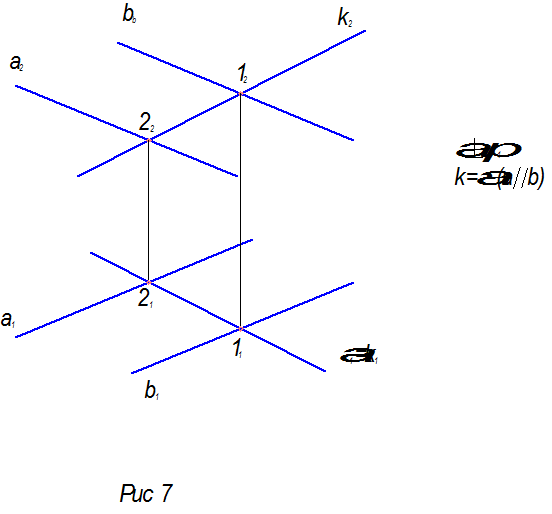
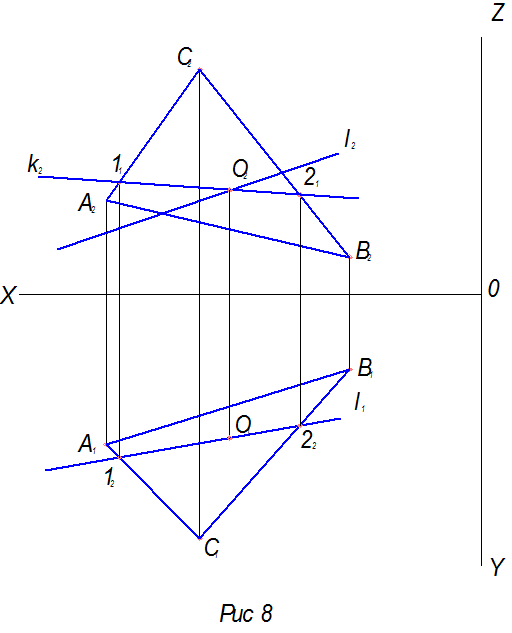
3) Точка пересечения построенной прямой пересечения плоскостей с заданной прямой и есть точка пересечения прямой с плоскостью (рис.8).