Парабола и ее свойства
Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax2, где х и у - текущие координаты, а- нек. число, наз. параболой.
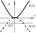 Если вершина нах. в О(0,0), то ур-е примет вид
Если вершина нах. в О(0,0), то ур-е примет вид
y2=2px-симметрично отн. оси ОХ
х2=2pу-симметрично отн. оси ОУ
Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса.
Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2
Св-ва:
1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax2.
5.1. Канонические и параметрические уравн прямой. Урав прямой, проходящ через две точки. 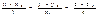

l m n
S{x2-x1,y2-y1,z2-z1}
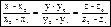
Каноническое уравнение прямой в пространстве:
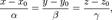
где 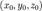 — координаты некоторой фиксированной точки
— координаты некоторой фиксированной точки 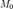 , лежащей на прямой,
, лежащей на прямой, 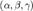 - координаты вектора, коллинеарного этой прямой.
- координаты вектора, коллинеарного этой прямой.
Параметрические уравнения прямой могут быть записаны в виде:

где t — производный параметр, при этом
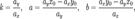
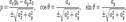
Сведение общего урав. прямой в пространсве к каноническим уравнениям.

P:A1x+B1y+C1z+D1=0
Q:A2x+B2y+C2z+D2=0
Общее ур-е прямой в пространстве.
Для того, чтобы перейти от общего к каноническому ур-ю прямой, надо задать начальную точку и направляющий вектор:
1. Найдем начальную точку:
Z=0 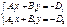
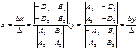
M0(x0,y0,0), т.к. Z=0
2. Найдем направляющий вектор S-?
P^N1{A1,B1,C1}
Q^N1{A2,B2,C2}
S=N1*N2
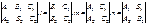
Взаимн распол-ние прямй и плоскоси. Угол между прямой и плоскостью
P:A1x+B1y+C1z+D1=0^N1{A1,B1}
Q:A2x+B2y+C2z+D2=0^N2{A2,B2}
а)
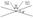
то 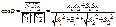
Взаимное расположение прямой и плоскости
Плоскость 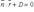 и прямая
и прямая 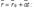
1) пересекаются 
2) прямая лежит в плоскости 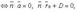
3) параллельны 
Если 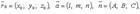 то случаи 1 - 3 имеют место, когда:
то случаи 1 - 3 имеют место, когда:
1) 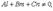
2) 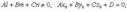
3) 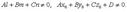
Нормальное уравнение плоскости. Расстояние от точки до плоскости.
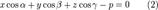
в векторной форме:
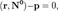
где 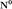 - единичный вектор,
- единичный вектор,  — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
— расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
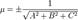
(знаки  и
и  противоположны).
противоположны).
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Расстояние  от точки
от точки 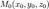 , до плоскости, заданной уравнением
, до плоскости, заданной уравнением  , вычисляется по формуле:
, вычисляется по формуле:
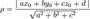
2,3 Уравнение плоскости, проходящей через три заданные точки  , не лежащие на одной прямой:
, не лежащие на одной прямой:
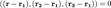
(смешанное произведение векторов), иначе
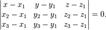
Способы задания прямой на плоскости: а)прям,проход-я через точку перпенд-но данному вектору; б)общ уравн в) урав в отрезках; г) урав прямой с угловым коэфф-нтом; д) урав прям, проходящ через точку в данном направлении.
Сначала запишем ур-е прямой, проходящей через заданную точку ^ заданному вектору.
 M0(x0,y0)
M0(x0,y0)

M0M{x-x0,y-y0}
n*M0M=0
A(x-x0)+B(y-y0)=0
Ax+By-Ax0-By0=0
-Ax0-By0=C
Ax+By+C=0-общее уравнение прямой на плоскости.
