Множество точек на плоскости, задаваемое характеристическими свойствами

Множество точек, которое можно назвать геометрической фигурой, может быть задано аналитическим условием, связывающим координаты этих точек. Такое соответствие служит основанием методов аналитической геометрии на плоскости. Например, множество

D = {(x, y): a < x < b, c < y < d} состоит из внутренних точек прямоугольника (рисунок 10).

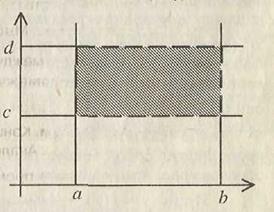
Рисунок 10

Обычно, если условие, определяющее множество точек плоскости, является равенством, связывающим переменные величины x и y, то это множество представляет собой кривую линию на плоскости. Так, множество

C = {(x, y): x² + y² = 25}

состоит из точек, находящихся на расстоянии 5 от начала координат, т.е. является окружностью радиуса 5. Множество, задаваемое условием K = {(x, y): x² + y² ≤ 25}, представляет собой внутренность круга радиуса 5, включая граничную окружность (поскольку неравенство в условии – нестрогое).

Замечание. Проверьте, что если в условии (*), задающем множество C, число 25 заменить числом 0, то множество C будет состоять из одной точки (0, 0), а если заменить его отрицательным числом (–1), то C будет пустым множеством.

Пример. Рассмотрим два множества точек на плоскости A = {(x, y): y ≤ x}, B = {(x, y): x < 2} (рисунок 11).

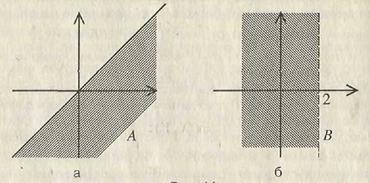
Рисунок 11

Первое множество состоит из всех точек, ордината которых меньше или равна абсциссе. Точки, для которых выполнено равенство x = y, образуют биссектрису 1-го и 3-го координатных углов. Точки множества А – полуплоскость, расположенная ниже (в данном случае можно сказать: правее) этой биссектрисы (рисунок 11, а). Множество В состоит из точек, абсцисса которых строго меньше 2, а ордината – любое число. Эти точки составляют полуплоскость, расположенную левее вертикальной прямой, проходящей через точку 2 на оси ОХ (рисунок 11, б). Тогда каждое из множеств A ∩ B, A È B, A \ B, B \ A представляет собой множество точек, заполняющих некоторый угол, образованный этими прямыми (рисунок 12, а, б, в, г).

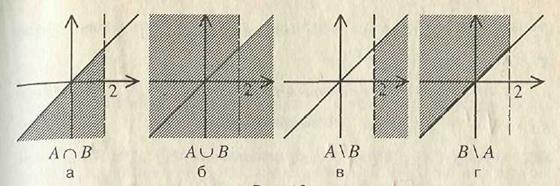
Рисунок 12

2. 2 Множества точек на плоскости, задаваемые уравнениями и неравенствами
с двумя переменными

Пусть на плоскости выбрана система координат. Тогда любое уравнение с двумя переменными F(x, y) = 0 задает множество точек на плоскости, а именно, множество точек М (х, у), координаты которых удовлетворяют этому уравнению. Например, точка М(–3, 4) принадлежит множеству, заданному уравнением x² + y² = 25, а точка N(1, 6) не принадлежит этому множеству
(в самом деле, (–3)² + 4² = 25, тогда как 1² + 6² ¹ 25). Из школьного курса известно, что уравнение
y = kx – b задает прямую, а уравнение y = ax² + bx + c при a ¹ 0 – параболу на плоскости. Точно так же любое неравенство с двумя переменными х и у задает какое-либо множество точек на плоскости. В частности, неравенство у > kx + b задает множество точек, лежащих выше прямой
(рисунок 13). Соответственно, неравенство у < kx + b задает множество точек, лежащих ниже прямой (рисунок 14). Здесь и далее линии, изображенные пунктиром, не включаются в соответствующее множество точек.

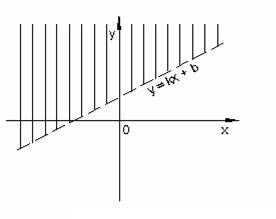
Рисунок 13

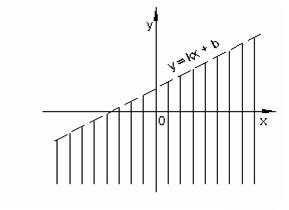
Рисунок 14

Аналогично неравенство y > ax² – bx + c задает множество точек, лежащих по одну сторону от параболы (рисунки 15 и 16), а неравенство y < ax² – bx +c задает множество точек, лежащих по другую сторону (рисунки 17 и 18).

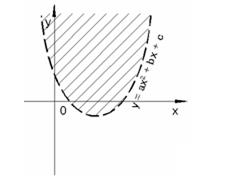
Рисунок 15

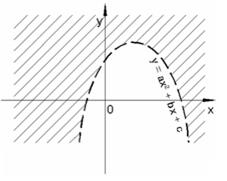
Рисунок 16

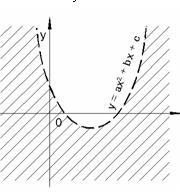
Рисунок 17

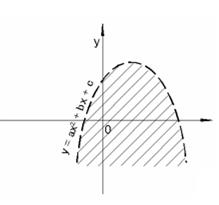
Рисунок 18

Когда имеется система уравнений или неравенств с двумя переменными, то множество решений такой системы представляет собой пересечение множеств решений каждого уравнения или неравенства, входящего в систему.

Пример. Построить множество точек, удовлетворяющих следующим соотношениям:

а) x < y £ x + 1;

б) .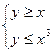

Решение. В случае а) соотношения равносильны следующей системе:

.

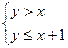Множество решений первого неравенства изображено штриховкой на рисунке 19, а второго неравенства – на рисунке 20. Прямая, изображенная на рисунке 19 пунктиром, означает, что точки на этой прямой не входят в множество решений неравенства. Множество решений системы есть пересечение двух множеств, оно изображено на рисунке 21.

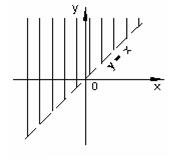
Рисунок 19

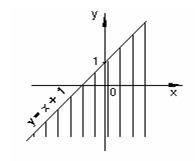
Рисунок 20

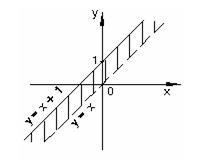
Рисунок 21

В случае б) множество решений первого неравенства изображено штриховкой на рисунке 22, второго неравенства – на рисунке 23, а множество точек, удовлетворяющих системе, – на рисунке 24.

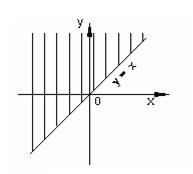
Рисунок 22

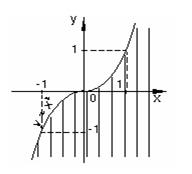
Рисунок 23

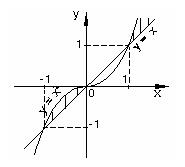
Рисунок 24