Уравнение прямой, проходящей через данную точку в данном направлении

Пусть прямая проходит через точку М(Хо,Уо) и ее направление характеризуется угловым коэффициентом к.

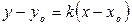
Уравнение с различными значениями к называют также уравнениеми пучка прямых с центром в точке М(Хо,Уо).

Уравнение прямой, проходящей через две точки.

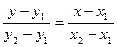, уравнение прямой, проходящей через две точки М₁(х1, у₁) и М₂(х₂,у₂)

Уравнение прямой в отрезках.

Пусть прямая пересекает ось Ох в точке М1(а,0), а ось Оу – в точке М2(0, b)

В этом случае уравнение примет вид: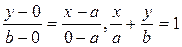

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

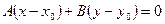- уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору.

5. нормальное уравнение прямой: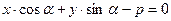

Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых: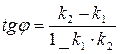

Расстояние от точки до прямой: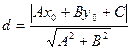

Плоскость в пространстве.

Простейшей поверхностью является плоскость. Плоскость в пространстве можно задавать различными способами. Каждому из них соответствует определенный вид ее уравнения.

1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору:

Точка Мо(Хо, Уо), вектор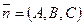

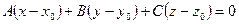
2. Уравнение плоскости, проходящей через три данные точки:

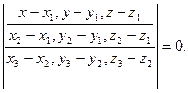
3. Нормальное уравнение плоскости: .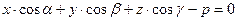

4. Угол между двумя плоскостями:

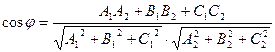
5. расстояние от точки до плоскости:

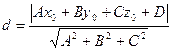
Уравнение плоскости в отрезках.

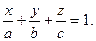
Прямая в пространстве.

1. Канонические уравнения прямой линии в пространстве, или уравнения прямой с направляющими коэффициентами, имеют вид:

.

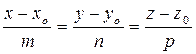где x0, y0, z0 - координаты точки, через которую проходит прямая, а m, n и p - направляющие коэффициенты прямой, которые являются проекциями на координатные оси Ox, Oy, Oz направляющего вектора прямой.

2. В параметрическом виде уравнения прямой линии в пространстве записываются так:

.

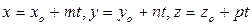3. Общие уравнения прямой:

А₁х +B₁y + C₁z + D₁=0

A₂x + B₂y + C₂z + D₂=0

4. Векторное уравнение прямой:

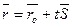
5. уравнение прямой в пространстве, проходящей через две точки:

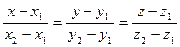
6. угол между прямыми:

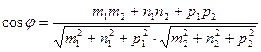
Взаимное расположение плоскостей.

Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей:
пусть заданы две плоскости Q₁ и Q₂:

А₁х +B₁y + C₁z + D₁=0

A₂x + B₂y + C₂z + D₂=0

Под углом между плоскостями понимается один из двугранных углов, образованных этими плоскостями.

.

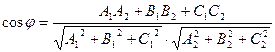Если плоскости перпендикулярны, то таковы же их нормали, т.е. 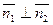. Но тогда 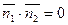,т.е.

A₁A₂ + B₁B₂ + C₁C₂ = 0. Полученное равенство есть условие перпендикулярности двух плоскостей.

Если плоскости параллельны, то будут параллельны и их нормали. Но тогда, как известно, координаты векторов пропорциональны: 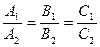. Это и есть условие параллельности двух плоскостей.