А),б) постановка задачи
Постановка задачи
Дано: приближенные значения а и b двух чисел
Определить: какое приближенное значение более точное (найти относительные погрешности приближений).
Решение
1) Найти приближенные значения чисел а и b с большим числом десятичных знаков а1 и b1.
2) Найти погрешность приближения 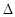 , как разность между двумя приближенными значениями.
, как разность между двумя приближенными значениями.
3) Определить предельные абсолютные погрешности 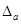 и
и 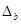 с избытком (округлить полученное значение погрешности приближения).
с избытком (округлить полученное значение погрешности приближения).
4) Найти предельные относительные погрешности приближений по формулам 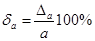 ,
, 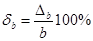
5) Сравнить относительные погрешности приближений двух чисел, сделать вывод.
№1 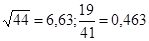 №2
№2 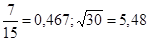
№3 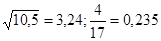 №4
№4 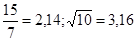
№5 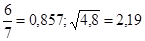 №6
№6 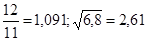
№7 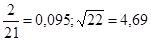 №8
№8 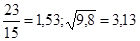
№9 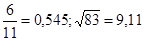 №10
№10 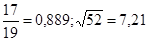
№11 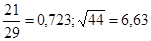 №12
№12 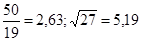
№13 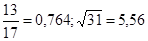 №14
№14 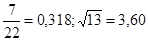
№15 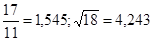 №16
№16 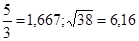
№17 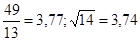 №18
№18 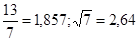
№19 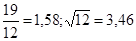 №20
№20 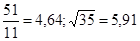
Задание 2. Округлить сомнительные цифры числа, оставив верные цифры: а) в строгом смысле; б) в широком смысле. Определить абсолютную погрешность результата.
А) Постановка задачи
Дано: приближенное значение числа и абсолютная погрешность приближения
Определить: округлить приближенное значение, оставив верные в строгом смысле знаки, определить абсолютную погрешность полученного приближения.
Решение
1) Определить верные в строгом смысле цифры данного приближенного значения, для чего сравнить абсолютную погрешность приближения с половиной каждого разряда, в котором стоят цифры данного числа.
2) Округлить данное приближенное значение по правилам округления, оставив только верные в строгом смысле цифры, и найти погрешность округления 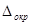 как разность между полученным после округления числом
как разность между полученным после округления числом 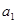 и данным приближенным значением числа
и данным приближенным значением числа 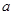 .
.
3) Найти предельную абсолютную погрешность приближения 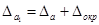
4) Сравнить полученную погрешность с половиной единицы разряда, в котором стоит последняя цифра числа 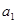 : если
: если 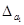 больше, чем это число, то нужно уменьшить число цифр в числе
больше, чем это число, то нужно уменьшить число цифр в числе 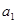 на одну по правилам округления и повторить 2) и 3) . Повторять этот процесс пока
на одну по правилам округления и повторить 2) и 3) . Повторять этот процесс пока 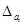 не будет меньше половины единицы разряда, в котором стоит последняя цифра числа
не будет меньше половины единицы разряда, в котором стоит последняя цифра числа 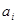 .
.
Б) Постановка задачи
Дано: приближенное значение числа 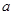 и
и 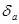 относительная погрешность приближения.
относительная погрешность приближения.
Определить: округлить приближенное значение, оставив верные в широком смысле знаки, определить абсолютную погрешность 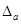 полученного приближения.
полученного приближения.
Решение
1. Найти относительную погрешность приближения 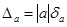
2. Найти верные в широком смысле цифры приближенного значения числа, сравнивая 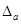 с единицей разряда, в котором стоит цифра приближенного значения числа.
с единицей разряда, в котором стоит цифра приближенного значения числа.
3. См. задачу а).
№1 а) 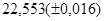 №11 а)
№11 а) 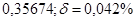
б) 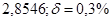 б)
б) 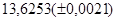
№2 а) 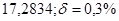 №12 а)
№12 а) 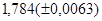
б) 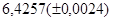 б)
б) 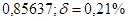
№3 а) 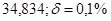 №13 а)
№13 а) 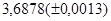
б) 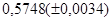 б)
б) 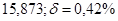
№4 а) 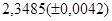 №14 а)
№14 а) 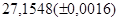
б) 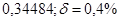 б)
б) 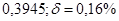
№5 а) 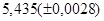 №15 а)
№15 а) 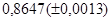
б) 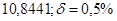 б)
б) 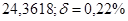
№6 а) 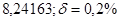 №16 а)
№16 а) 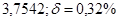
б) 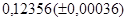 б)
б) 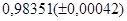
№7 а) 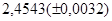 №17 а)
№17 а) 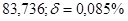
б) 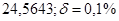 б)
б) 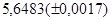
№8 а) 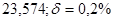 №18 а)
№18 а) 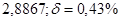
б) 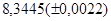 б)
б) 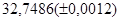
№9 а) 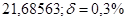 №19 а)
№19 а) 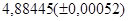
б) 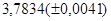 б)
б) 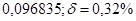
№10 а) 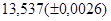 №20 а)
№20 а) 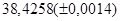
б) 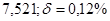 б)
б) 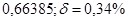
Задание 3 Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры: а) в узком смысле; б) в широком смысле.
№1 а) 0,2387; б) 42,884 №11 а) 18,357; б) 2,16
№2 а) 3,751; б) 0,537 №12 а) 0,5746; б) 236,58
№3 а) 11,445; б) 2,043 №13 а) 14,862; б) 8,73
№4 а) 2,3445; б) 0,745 №14 а) 0,3648; б) 21,7
№5 а) 8,345; б) 0,288 №15 а) 2,4516; б) 0,863
№6 а) 12,45; б) 3,4453. №16 а) 62,74; б) 0,389
№7 а) 0,374; б) 4,348 №17 а) 5,6432; б) 0,00858
№8 а) 20,43; б) 0,576 №18 а) 0,0384; б) 63,745
№9 а) 41,72; б) 0,678 №19 а) 12,688; б) 4,636
№10 а) 5,634; б) 0,0748 №20 а) 6,743; б) 0,543
Задание 4. а), б) Вычислить и определить погрешности результата.
а),б) Постановка задачи
Дано: приближенные значения чисел и абсолютные погрешности приближений.
Найти: значение формулы и абсолютную и относительную погрешности результата.
Решение.
1) Найти приближенное значение формулы.
2) Найти относительные погрешности приближений всех данных чисел.
3) Воспользовавшись формулами действия над относительными погрешностями определить погрешность результата.
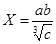
№1 а =3,85(±0,001); b = 2,0435(±0,0004); с = 962,6(±0,1)
№2 а =4,16(±0,005); b = 12,163(±0,002); с = 55,18(±0,03)
№3 а =7,27(±0,01); b = 5,205(±0,002); с = 87,32(±0,03)
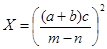
№4 а =4,3(±0,05); b = 17,21(±0,02); с = 8,2(±0,05); m = 12,417(±0,003);
n = 8,37(±0,005)
№5 а =5,2(±0,04); b = 15,32(±0,01); с = 7,5(±0,05); m = 21,823(±0,002);
n = 7,56(±0,005)
№6 а =2,13(±0,01); b = 22,16(±0,03); с = 6,3(±0,04); m = 16,825(±0,004);
n = 8,13(±0,002)
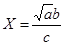
№7 а =228,6(±0,06); b = 86,4(±0,02); с = 68,7(±0,05)
№8 а =315,6(±0,05); b = 72,5(±0,03); с = 53,8(±0,04)
№9 а =185,7(±0,04); b = 66,6(±0,02); с = 72,3(±0,03)
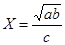
№10 а =3,845(±0,004); b = 16,2(±0,05); с = 10,8(±0,1)
№11 а =4,632(±0,003); b = 23,3(±0,04); с = 11,3(±0,06)
№12 а =7,3127(±0,004); b = 18,4(±0,03); с = 20,2(±0,08)
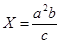
№13 а =1,245(±0,002); b = 0,642(±0,0005); с = 7,12(±0,004)
№14 а =1,245(±0,001); b = 0,121(±0,0002); с = 2,34(±0,003)
№15 а =0,327(±0,005); b = 3,147(±0,0001); с = 1,78(±0,001)
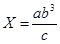
№16 а =0,643(±0,0005); b = 2,17(±0,002); с = 5,843(±0,001)
№17 а =0,142(±0,0003); b = 1,71(±0,002); с = 3,727(±0,001)
№18 а =0,258(±0,0002); b = 3,45(±0,001); с = 7,221(±0,003)
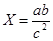
№19 а =0,3575(±0,0002); b = 2,63(±0,01); с = 0,854(±0,0005)
№20 а =0,1756(±0,0001); b = 3,71(±0,03); с = 0,285(±0,0002)
