Уравнение Лапласа и Пуассона

Оглавление

Оглавление. 1

1. Уравнение Лапласа и Пуассона. 2

a)Физический смысл стационарной задачи. 2

b)Примеры. . 2

c)Понятие о потенциалах. 2

d)Постановка задач. 2

2. Первая и вторая формулы Грина с оператором 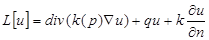, следствия. 3

3. Гармонические функции. Интегральное представление. Их основные свойства. 4

4. Теорема о среднем для гармонических функций.. 6

5. Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле. 7

6. Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений. 8

7. Функция Грина для задачи с уравнением 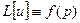, понятия, определения. 9

a)решение задач с её помощью.. 9

b)построение в одномерном случае на отрезке. 9

8. Теория потенциалов, определение, основные свойства. 11

a)Объёмный потенциал. 12

b)Потенциал простого слоя. 14

c)Потенциал двойного слоя. 15

d)Решение задач Дирихле с уравнением Пуассона методом теории потенциалов. 16

e)Сводная таблица6 общие сведения о потенциалах: 17

9. Понятие о корректно и некорректно поставленных задачах математической физики, примеры. 18

10.Уравнение с оператором 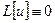с особенностью 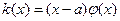, свойства, ограниченность, постановка задачи. 19

11.Уравнение Бесселя. 20

a)особенность, построение ограниченного решения 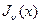. 21

b)общее решение, 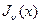, , 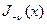, 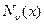понятие о функциях 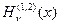. 22

c)асимптотика решений уравнения Бесселя, нули функции Бесселя. 23

d)краевая задача на собственные значения: 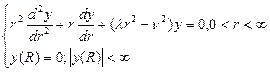, её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д. 24

e)модифицированное уравнение Бесселя, ограниченность решения 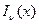, свойства, общее решение, понятие о функции 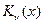. 25

f)Сводная таблица. 26

12.Краевая задача 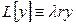с двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора 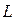. 27

13.Уравнение гипергеометрического типа. 28

a)Приведение к самосопряжённому виду. Весовые функции 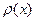. Уравнение для производных. 28

b)Решение в виде полиномов. Формула Родрига. 29

c)Ортогональные решения полиномов.Свойства нулей. 30

14.Примеры: уравнения, краевые задачи, определение и свойства полиномов. 31

a)Лежандра. 31

b)Чебышева-Лягера. 32

c)Чебышева-Эрмита. 33

d)Сводная таблица для уравнений гипергеометрического вида. 34

15.Уравнения, краевая задача для присоединенных полином Лежандра. Решения. Основные свойства. 36

16.Уравнение Лапласа в сферических координатах. Схема решения методом разделения переменных. 37

17.Сферические функции, определения, построение системы базисных функций. Ортогональность, полнота, теорема о разложении, б/д. 38

Уравнение Лапласа и Пуассона.

Уравнение вида: 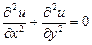или 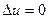- называется уравнением Лапласа.

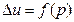- неоднородное уравнение Лапласа – уравнение Пуассона.

Обобщим эти уравнения: 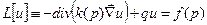, где р – некоторая точка трёхмерного пространства.