Векторное произведение
Введем, в первую очередь, следующее понятие.
Определение.Упорядоченная тройка векторов  ,
,  ,
,  называется правой, если, будучи отложенными из одной точки, они направлены таким образом, что глядя с конца вектора
называется правой, если, будучи отложенными из одной точки, они направлены таким образом, что глядя с конца вектора  на плоскость, образованную векторами
на плоскость, образованную векторами  и
и  , кратчайший поворот от вектора
, кратчайший поворот от вектора  к вектору
к вектору  будет осуществляться против часовой стрелки. В обратном случае указанная тройка векторов называется левой.
будет осуществляться против часовой стрелки. В обратном случае указанная тройка векторов называется левой.
Примером правой тройки векторов может служить упорядоченная тройка единичных ортов 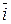 ,
, 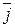 ,
, 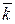 .
.
Определение.Векторным произведением вектора  на вектор
на вектор  (обозначается
(обозначается 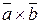 ) называется вектор
) называется вектор  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) вектор  перпендикулярен и вектору
перпендикулярен и вектору  , и вектору
, и вектору  ;
;
2) длина вектора  определяется равенством:
определяется равенством:
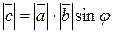 ,
,
где 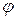 - угол между векторами
- угол между векторами  и
и  ;
;
3) тройка векторов  ,
,  ,
,  - правая.
- правая.
 Заметим, что второе условие последнего определения означает, что длина векторного произведения равна площади параллелограмма, построенного на перемножаемых векторах, если отложить их из одной точки.
Заметим, что второе условие последнего определения означает, что длина векторного произведения равна площади параллелограмма, построенного на перемножаемых векторах, если отложить их из одной точки.
Рассмотрим основные свойства векторного произведения.
1. Векторное произведение равно нулевому вектору тогда и только тогда, когда либо векторы коллинеарны, либо один из них является нулевым.
Доказательство. Из определения нулевого вектора следует, что векторное произведение равно такому вектору тогда и только тогда, когда длина векторного произведения равна нулю:
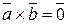
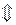
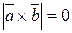
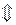
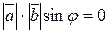 .
.
Последнее произведение равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю, т.е. когда либо вектор  - нулевой, либо вектор
- нулевой, либо вектор  - нулевой, либо
- нулевой, либо 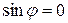 . Условие
. Условие 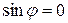 равносильно тому, что векторы
равносильно тому, что векторы  и
и  - коллинеарны. ■
- коллинеарны. ■
2. Для любых векторов  и
и  выполняется равенство:
выполняется равенство:
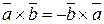 .
.
Доказательство. Данное утверждение непосредственно следует из определения векторного произведения с учетом того, что если поменять векторы  и
и  в векторном произведении местами, то изменится ориентация тройки, а именно
в векторном произведении местами, то изменится ориентация тройки, а именно 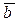 ,
, 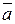 ,
, 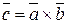 - левая тройка векторов. Так как при этом не меняются длина векторного произведения, а меняется лишь на противоположное его направление, то
- левая тройка векторов. Так как при этом не меняются длина векторного произведения, а меняется лишь на противоположное его направление, то
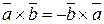 . ■
. ■
3. Для любых векторов  ,
,  и для любого числа
и для любого числа 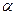 справедливо равенство:
справедливо равенство:
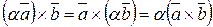 .
.
Доказательство. Докажем равенство
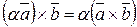 .
.
Оно очевидно выполняется, если один из векторов  ,
,  является нулевым или число
является нулевым или число 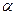 равно нулю. Пусть
равно нулю. Пусть 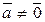 ,
,  ,
, 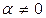 . Покажем, что векторы
. Покажем, что векторы 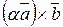 и
и 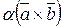 имеют одинаковую длину. По определению векторного произведения имеем:
имеют одинаковую длину. По определению векторного произведения имеем:
 ,
,
где 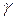 - угол между векторами
- угол между векторами 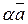 и
и  . При этом угол
. При этом угол 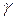 равен углу
равен углу 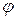 между векторами
между векторами  и
и  , если
, если 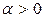 , и равен углу
, и равен углу 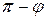 , если
, если 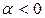 . В любом случае получаем:
. В любом случае получаем:
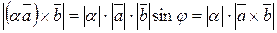 .
.
Кроме того, векторы 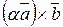 и
и 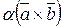 имеют одно и то же направление – направление вектора
имеют одно и то же направление – направление вектора 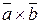 , если
, если 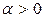 , и направление вектора
, и направление вектора 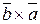 . Если
. Если 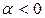 . Таким образом
. Таким образом
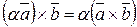 .
.
Аналогично показывается, что
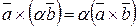 . ■
. ■
4. Для любых векторов  ,
,  и
и  справедливо равенство:
справедливо равенство:
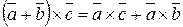 .
.
Доказательство. Если вектор  - нулевой, то доказываемое равенство очевидно. Пусть теперь
- нулевой, то доказываемое равенство очевидно. Пусть теперь 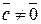 . Рассмотри единичный вектор
. Рассмотри единичный вектор 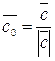 . Отложим векторы
. Отложим векторы  и
и 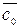 из одной точки
из одной точки 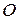 и построим плоскость, проходящую через точку
и построим плоскость, проходящую через точку 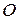 и перпендикулярную вектору
и перпендикулярную вектору 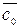 . Пусть
. Пусть 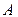 - конец вектора
- конец вектора  , а
, а 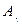 - проекция точки
- проекция точки 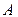 на построенную плоскость. Повернем вектор
на построенную плоскость. Повернем вектор 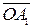 вокруг точки
вокруг точки 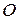 в указанной плоскости на
в указанной плоскости на 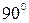 по часовой стрелке, если смотреть с конца вектора
по часовой стрелке, если смотреть с конца вектора 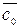 . В результате получим вектор
. В результате получим вектор 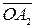 . Покажем, что
. Покажем, что 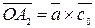 . Действительно,
. Действительно,
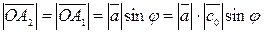 ,
,
где 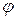 - угол между вектором
- угол между вектором  и вектором
и вектором  . При этом вектор
. При этом вектор 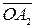 перпендикулярен и вектору
перпендикулярен и вектору  и вектору
и вектору 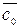 . В соответствии с построением тройка
. В соответствии с построением тройка  ,
, 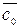 ,
, 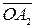 является правой. Следовательно,
является правой. Следовательно,
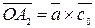 .
.
Отложим вектор  из точки
из точки 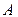 . Пусть при этом
. Пусть при этом 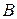 - конец вектора
- конец вектора  . По определению суммы векторов имеем:
. По определению суммы векторов имеем:
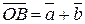 .
.
Пусть 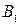 - проекция точки
- проекция точки 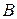 на построенную плоскость. Повернем вектор
на построенную плоскость. Повернем вектор 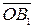 вокруг точки
вокруг точки 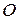 в указанной плоскости на
в указанной плоскости на 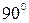 по часовой стрелке, если смотреть с конца вектора
по часовой стрелке, если смотреть с конца вектора 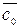 . Получим вектор
. Получим вектор 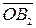 . По аналогии получаем:
. По аналогии получаем:
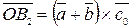 ,
,
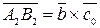 .
.
Так как
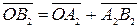 ,
,
То в результате будем иметь:
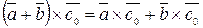
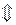
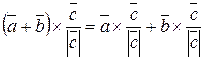 .
.
Умножим обе части полученного равенства на 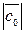 . В итоге получаем требуемое равенство:
. В итоге получаем требуемое равенство:
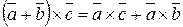 . ■
. ■
На практике при нахождении векторного произведения обычно пользуются следующим утверждением.
Теорема.Пусть в ортонормированном базисе 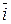 ,
, 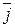 ,
, 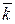 заданы два вектора:
заданы два вектора:
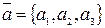 ,
,
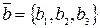 .
.
Тогда векторное произведение 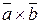 может быть найдено по формуле:
может быть найдено по формуле:
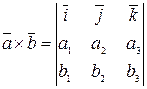 .
.
Доказательство. Воспользуемся свойствами 3,4 векторного произведения. В соответствии с ними получим:
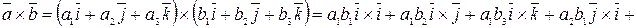
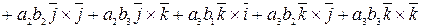 .
.
Из свойства 1 векторного произведения следует:
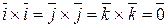 .
.
Кроме того, так как система векторов 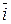 ,
, 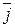 ,
, 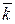 - ортонормированная с правой ориентацией, то справедливы равенства:
- ортонормированная с правой ориентацией, то справедливы равенства:
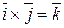 ,
,
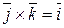 ,
,
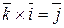 .
.
С учетом свойства 2 векторного произведения в результате получаем:
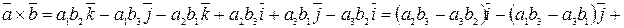
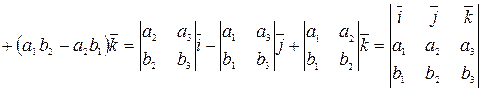 ,
,
что и требовалось доказать. ■
Пример.Даны вершины треугольника 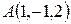 ,
, 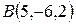 и
и 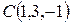 . Вычислить площадь этого треугольника и длину его высоты, опущенной из вершины
. Вычислить площадь этого треугольника и длину его высоты, опущенной из вершины 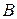 .
.
∆ Найдем векторы 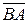 и
и 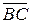 :
:
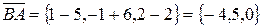 ,
,
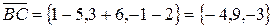 .
.
Для нахождения площади треугольника найдем векторное произведение 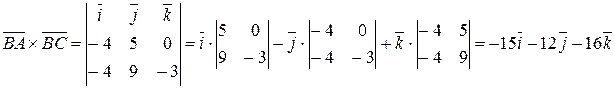 .
.
Из определения векторного произведения следует, что площадь параллелограмма, построенного на найденных векторах, равна длине их векторного произведения. Следовательно, площадь треугольника 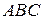 равна половине площади этого параллелограмма и, соответственно, равна
равна половине площади этого параллелограмма и, соответственно, равна
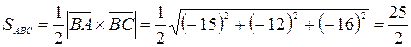 .
.
Для нахождения высоты, опущенной из вершины 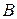 , найдем длину основания
, найдем длину основания 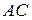 :
:
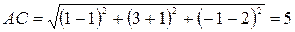 .
.
Воспользуемся известной формулой нахождения площади треугольника через его высоту:
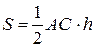 ,
,
где 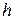 - высота треугольника, опущенная из вершины
- высота треугольника, опущенная из вершины 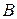 . Следовательно, высота определяется следующим образом:
. Следовательно, высота определяется следующим образом:
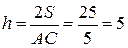 . ▲
. ▲
