Векторное произведение и его св-ва.

Векторным произведением двух ненулевых векторов а и в взятых в указанном порядке, называется вектор с, удовлетворяющий условие:

- длина вектора с, численно равна площади параллелограмма, построенного на перемножающих векторах как на сторонах.

|c| = |a| * |b| *sin(phi) ; phi = (a;^ b);

- тройка векторов а,b,c – должна быть правой.

Св-ва векторного произведения:

1.) Векторное произведение антиперестановочно: a x b = - (b x a).

2.) a x (b + c) = a x b + a x c

Распределительный закон векторного умножения.

3.) ( ,\a) x b = a x ( ,\) b) = ,\ * ( a x b)

Сочетательный закон векторного умножения.

4.) Условие коллинеарностей векторов:

Теорема: Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулю(0).

a не(=) 0; b не(=) 0; a II b ó a x b = 0.

14.) * Выражение скалярного произведения через координаты сомножителей.

Пусть даны два вектора в координатном пространстве: a = ax*i + ay*j + az*k; b = bx*i + by*j + bz*k;

Распределительный и сочитательный законы векторного произведения позволяют вектор a и b, перемножить векторно как многочлены.

a x b = (ax*i + ay*j + az*k) x (bx*i + by*j + bz*k).

a x b = ax*bx*(i*i) + ax*by*(i*j) + ax*bz*(i*k) + ay*bx*(j*i) + ay*by*(j*j) + ay*bz*(j*k) + az*bx*(k*i) + az*by*(k*j) + az*bz*(k*k).

1.) i x i = 0; j x j = 0; k x k = 0. В силу коллинеарности.

Покажем, что i x j = k.

По определению векторного произведения:

1.) |i x j| = |i| * |j| * sin(90’) = 1 , но и |k| = 1.

2.) (i x j) _I_ i и ( i x j) _I_ j , но и k _I_ i и k _I_ j.

3.) i, j, i x j - правая тройка, но и i, j, k - правая тройка.

Таким образом, i x j = k , но тогда j x i = - k.

Аналогично, j x k = i ; и k x j = - i;

k x i = j ; и i x k = - j;

В связи с этим:

a x b = ax*by*k – ax*bz*j – ay*bx*k + ay*bz*i + az*bx*j – az*by*i , откуда

a x b = (ay*bz – az*by)*i + (az*bx – ax*bz)*j + (ax*by – ay*bx)*k. Формула ( 4.1)

Формула (4.1) определяет выражение векторного произведения через координаты сомножителей. Эту формулу можно получить разложением условного определителя 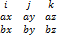по элементам первой строки.

Приложения векторного произведения.

1’) Установление коллинеарности ненулевых векторов.

a x b = 0 - условие коллинеарности в векторной форме =>

.

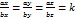2’) Вычисление площади параллелограмма и треугольника.

Sпар. = |a| * |b| * sin(phi) , phi (a;^b);

Sпар. = ½ * |a| * |b| * sin(phi).

3’) Нахождение момента силы (F)/

Момент силы (М), силы (F), приложенный в точке т.А, будет:

F= OA x F.

4’) Определением линейной скорости вращения.

Пусть т.М произвольная точка твёрдого тела, вращающаяся вокруг неподвижной оси, то линейная скорость V, в т. М будет определяться равенством:

V = W x OM; V = w x r.

Смешанное произведение и его св-ва.

Смешанным произведением трёх ненулевых векторов, называется произведение в котором первые два умножаются векторно, а их результат на третий умножается скалярно.

(a x b) * c [a x b] * c (a x b, c).

Результатом смешанного произведения является число, т.к. последняя операция при его составлении скалярное произведение.

Если хотя бы один из векторов равен нулю, то смешанное произведение равно нулю.

Св-ва смешанного произведения:

1’) Смешанное произведение не изменяется при круговой перестановке векторов.

( a x b , c) = ( b x c , a) = ( c x a , b).

т.к. смешанное произведение не зависит от того, какие два вектора перемножаются векторно, его обозначать …… (a,b,c)

2’) При некруговой перестановке векторов, смешанное произведение изменяет свой знак на противоположный.

(a , b , c) = - ( a , c , b).

3’) Условие компланарности трёх ненулевых векторов:

Теорема: Три ненулевых вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.