Векторы и действия с ними

Вопросы для подготовки к экзамену по математике

I семестр

Элементы линейной алгебры

Матрицы и действия с ними

1. Матрицы.

2. Линейные операции над матрицами. Транспонирование матриц.

3. Умножение матриц.

4. Обратная матрица.

1.В каком месте матрицы 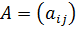расположен элемент ?

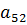2.Может ли матрица состоять: а) из одной строки; б) из одного столбца; в) из одной строки и одного столбца?

3.Может ли какой-нибудь элемент диагональной матрицы быть равным нулю?

4.Могут ли быть равными квадратные матрицы, одна из которых третьего порядка, а другая - четвертого?

5.Можно ли найти сумму двух матриц, одна из которых имеет размер 3х4, а другая – размер 4х3?

6.Существует ли произведение матриц АВ, если матрица А имеет размер 3х4, а матрица В – размер 4х2? Существует ли для этих матриц произведение ВА?

7.Можно ли найти произведение двух матриц, одна из которых квадратная, а другая не является квадратной?

8.Пусть для матриц А и В существуют произведения АВ и ВА. Можно ли утверждать, что матрицы АВ и ВА одного размера?

9.Может ли произведение двух ненулевых матриц быть нулевой матрицей?

Определители

1. Определители, их свойства.

2. Миноры и алгебраические дополнения.

3. Применение определителей.

4. Ранг матрицы.

1.При каких условиях определитель матрицы второго порядка равен нулю?

2.С каким знаком в определитель матрицы четвертого порядка входит слагаемое ?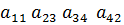

3.Может ли произведение 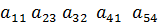, взятое с соответствующим знаком, быть членом определителя матрицы пятого порядка?

4.Чем отличается минор 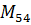от алгебраического дополнения ?

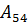5.Пусть матрица А содержит минор пятого порядка, отличный от нуля. Что можно сказать о ранге матрицы А?

6. Чему равна сумма произведений элементов какой-нибудь строки матрицы на алгебраические дополнения элементов другой строки этой матрицы?

7. Как находить ранг матрицы?

8.Может ли ранг матрицы А размера 7х3 равняться четырем?

Системы линейных уравнений

1. Системы линейных уравнений и методы их решения.

2. Совместность систем линейных уравнений.

3. Однородные системы линейных уравнений.

1.Что называется общим и частным решениями системы линейных уравнений?

2.К каким системам линейных уравнений применимы правило Крамера и матричный способ?

3.К каким системам линейных уравнений применим метод Гаусса, в чем он заключается?

4.Может ли однородная система линейных уравнений быть несовместной?

5. При каких условиях однородная система имеет ненулевые решения?

Векторы и действия с ними.

1. Векторы. Линейные операции над векторами.

2. Скалярное произведение векторов, его свойства.

3. Векторное произведение и его свойства.

4. Линейная зависимость векторов.

5. Базис системы векторов.

6. Разложение вектора по базису.

1.Могут ли быть равными два вектора, один из которых –четырехмерный, а другой – пятимерный?

2.Какие векторы получаются из вектора умножением на число 0 и -1?

3.Какие векторы называются линейно независимыми?

4.Будет ли система векторов 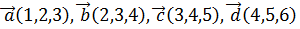линейно независимой?

5.Образуют ли векторы 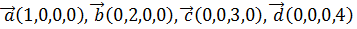базис пространства ?

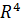6.Какие числа называются координатами вектора в данном базисе?

7.При каком значении 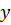скалярное произведение векторов 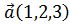и 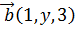равно нулю?

8.При каких значениях 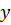векторы 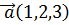и 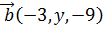образуют линейно независимую систему?