Понятие определенного интеграла, его геометрический смысл. Нижняя и верхняя интегральные суммы
Пусть функция 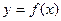 определена на отрезке
определена на отрезке 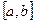 ,a<b. Разобьем этот отрезок на n произвольных частей точками
,a<b. Разобьем этот отрезок на n произвольных частей точками
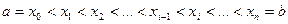
Обозначим это разбиение через 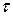 , а точки
, а точки 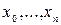 будем называть точками разбиения. В каждом из полученных частичных отрезков
будем называть точками разбиения. В каждом из полученных частичных отрезков 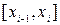 выберем произвольную точку
выберем произвольную точку 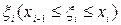 . Через
. Через 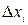 обозначим разность
обозначим разность 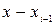 , которую будем называть длиной частичного отрезка
, которую будем называть длиной частичного отрезка 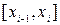 .
.
Составим сумму
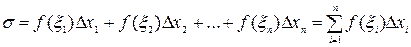 (1)
(1)
которую назовем интегральной суммой для функции f(x) на [a,b], соответствующей данному разбиению [a,b] на частичные отрезки и данному выбору промежуточных
точек 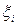 . Геометрический смысл суммы очевиден: это сумма площадей прямоугольников с основаниями
. Геометрический смысл суммы очевиден: это сумма площадей прямоугольников с основаниями 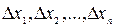 и высотами
и высотами 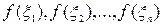 , если f(x)>=0.
, если f(x)>=0.
Обозначим через 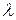 длину наибольшего частичного отрезка разбиения
длину наибольшего частичного отрезка разбиения 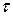 :
: 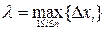 .
.
Определение:Если существует конечный предел I интегральных сумм (1) при 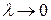 , то этот предел называется определенным интегралом от функции f(x) по отрезку [a,b] и обозначается следующим образом:
, то этот предел называется определенным интегралом от функции f(x) по отрезку [a,b] и обозначается следующим образом:
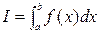 т.е.
т.е.
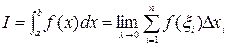
В этом случае функция f(x) называется интегрируемой на [a,b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, x – переменной интегрирования.
Билет 14.
Свойства определенного интеграла
- По определению
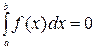
- По определению
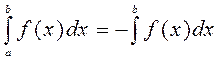
- Каковы бы ни были числа a, b, c, всегда имеет место равенство
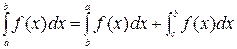
- Постоянный множитель можно выносит за знак определенного интеграла, т.е.
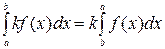
- Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е.
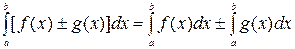
Формулы оценки определенных интегралов
Будем полагать, что 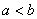 .
.
1. Если 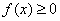 всюду на отрезке
всюду на отрезке 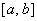 , то
, то 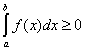 .
.
2. Если 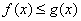 всюду на отрезке
всюду на отрезке 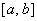 , то
, то 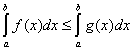 .
.
3. Если 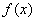 интегрируема на отрезке
интегрируема на отрезке 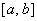 , то
, то 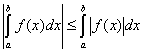 .
.
4. Если 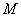 и
и 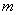 - соответственно максимум и минимум функции
- соответственно максимум и минимум функции 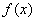 на отрезке
на отрезке 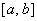 , то
, то
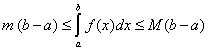 .
.
Билет 15.
Определенный интеграл как функция верхнего предела
Если функция 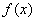 интегрируема на отрезке
интегрируема на отрезке 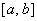 , то она интегрируема и на отрезке
, то она интегрируема и на отрезке 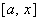 , где
, где 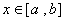 . Рассмотрим функцию аргумента
. Рассмотрим функцию аргумента 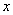
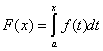 . (1)
. (1)
Назовем функцию 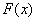 интегралом с переменным верхним пределом. В формуле (1) переменная интегрирования обозначена буквой
интегралом с переменным верхним пределом. В формуле (1) переменная интегрирования обозначена буквой 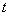 , чтобы избежать путаницы с переменным верхним пределом
, чтобы избежать путаницы с переменным верхним пределом 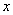 .
.
Теорема: Непрерывная на отрезке 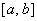 функция
функция 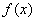 имеет на этом отрезке первообразную. Одной из первообразных является функция
имеет на этом отрезке первообразную. Одной из первообразных является функция
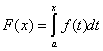 .
.
Таким образом, любая непрерывная на отрезке 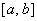 функция
функция 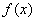 имеет на этом отрезке первообразную в форме определенного интеграла
имеет на этом отрезке первообразную в форме определенного интеграла 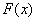 с переменным верхним пределом. Поскольку всякая другая первообразная отличается от
с переменным верхним пределом. Поскольку всякая другая первообразная отличается от 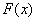 на постоянную величину, то связь между неопределенным и определенным интегралами имеет вид
на постоянную величину, то связь между неопределенным и определенным интегралами имеет вид
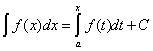 ,
,
где С – произвольная постоянная.
Билет 16.
