Классификаия неньютоновских жидкостей
Наиболее простой классификацией неньютоновских жидкостей является классификация американских ученых Д.Доджа и А.Метцнера. Они группирует неньютоновские системы по трем основным категориям:
- неньютоновские вязкие жидкости, где скорости сдвига зависят только от приложенных напряжений;
- жидкости, реологические характеристики которых зависят от времени. В этих системах скорость сдвига определяется не только величиной касательного напряжения, но и продолжительностью его действия;
- вязкоупругие жидкости, проявляющие одновременно свойства вязкой жидкости и упругого тела.
а) Вязкопластичные жидкости. Реологическое уравнение вязкопластичной жидкости в случае одномерного течения можно записать в виде:
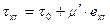 , если
, если 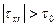 , (11.1)
, (11.1)
где 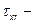 касательное напряжение трения между слоями жидкости, движущимися в направлении оси
касательное напряжение трения между слоями жидкости, движущимися в направлении оси 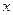 параллельно стенкам круглой трубы;
параллельно стенкам круглой трубы; 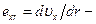 скорость деформации (в данном случае скорость сдвига);
скорость деформации (в данном случае скорость сдвига); 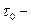 предельное напряжение сдвига;
предельное напряжение сдвига; 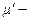 пластическая или структурная вязкость. Если
пластическая или структурная вязкость. Если 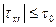 текучесть отсутствует, т.е. среда ведет себя как твердое тело (
текучесть отсутствует, т.е. среда ведет себя как твердое тело ( 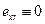 ). Согласно этой модели, называемой моделью Бингама-Шведова, среда не деформируется, если
). Согласно этой модели, называемой моделью Бингама-Шведова, среда не деформируется, если 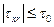 , в противном случае жидкость ведет себя, как ньютоновская вязкая жидкость, однако под действием напряжений, избыточных по отношению к
, в противном случае жидкость ведет себя, как ньютоновская вязкая жидкость, однако под действием напряжений, избыточных по отношению к 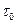 , а именно,
, а именно, 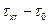 .
.
В приложении к высокопарафинистой нефти такие необычные свойства вязкопластичной жидкости Бингама-Шведова чаще всего связывают с существованием в жидкости некоторой жесткой пространственной структуры. Такая структура образуется, когда жидкость неподвижна, и затем она сопротивляется внешнему воздействию, стремящемуся привести жидкость в движение. Сопротивление происходит до тех пор, пока напряжение сдвига, вызванное внешним воздействием, не превзойдет некоторой величины 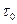 . Когда это происходит, жесткая структура полностью разрушается, и среда ведет себя как обычная ньютоновская жидкость под действием напряжения
. Когда это происходит, жесткая структура полностью разрушается, и среда ведет себя как обычная ньютоновская жидкость под действием напряжения 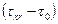 . Однако жесткая структура восстанавливается вновь, если действующее напряжение
. Однако жесткая структура восстанавливается вновь, если действующее напряжение 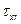 сдвига становится меньше
сдвига становится меньше 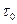 .
.
Иными словами, сдвиговое течение вязкопластичных жидкостей характеризуется образованием застойных зон в тех областях потока жидкости, в которых касательные напряжения меньше предельного напряжения сдвига.
Модель вязкопластичной жидкости используется для описания поведения глинистых растворов, ряда нефтей, шламов, масляных красок и т.д. Кривая течения вязкопластичных жидкостей представлена на рис. 11.1.
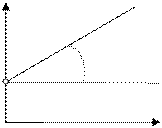
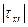
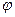
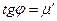
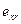
Рис. 11.1.Кривая течения вязкопластичной жидкости
б) Степенные жидкости. Реологическое уравнение степенной неньютоновской жидкости в случае одномерного сдвигового течения можно записать в виде уравнения
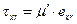 ,
,
внешне похожего на уравнение (2.5) ньютоновской вязкой жидкости. Однако для неньютоновской жидкости параметр 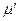 не является константой модели, а зависит от структуры течения. Если, предположить, например, что параметр
не является константой модели, а зависит от структуры течения. Если, предположить, например, что параметр 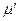 , являющийся скалярной величиной, зависит только от модуля скорости сдвига
, являющийся скалярной величиной, зависит только от модуля скорости сдвига 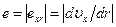 и зависимость эта степенная, то можно написать:
и зависимость эта степенная, то можно написать:
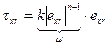 , т.е.
, т.е. 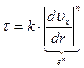 , (11.2)
, (11.2)
причем знак напряжения 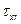 совпадает со знаком скорости сдвига
совпадает со знаком скорости сдвига 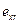 так же, как это имеет место в модели ньютновской вязкой жидкости. Здесь
так же, как это имеет место в модели ньютновской вязкой жидкости. Здесь 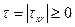 . В законе (11.2) показатель степени
. В законе (11.2) показатель степени 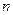 называют индексом течения, а коэффициент
называют индексом течения, а коэффициент 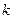 - консистентностью жидкости; если
- консистентностью жидкости; если 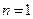 , эта модель переходит в модель ньютоновской вязкой жидкости, причем
, эта модель переходит в модель ньютоновской вязкой жидкости, причем 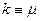 .
.
В зависимости от хода кривой течения относительно осей 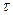 и
и 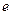 возможны два типа таких жидкостей: псевдопластичные, для которых кривая течения выпукла вверх
возможны два типа таких жидкостей: псевдопластичные, для которых кривая течения выпукла вверх 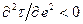 (
( 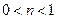 ), и дилатантные, для которых кривая течения выпукла вверх
), и дилатантные, для которых кривая течения выпукла вверх 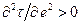 (
( 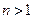 ) (рис. 11.2).
) (рис. 11.2).
Параметр 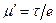 называют кажущейся вязкостью. У псевдопластичных жидкостей
называют кажущейся вязкостью. У псевдопластичных жидкостей 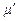 постепенно уменьшается, у дилатантных возрастает.
постепенно уменьшается, у дилатантных возрастает.
Свойствами псевдопластичности, обладают, например, суспензии с асимметричными частицами. Предполагается, что с возрастанием скорости сдвига асимметричные частицы постепенно ориентируются своими большими осями вдоль направления течения. При увеличении скорости сдвига кажущаяся вязкость 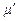 убывает до тех пор, пока сохраняется возможность дальнейшего ориентирования частиц вдоль линий тока, а затем, когда такая возможность исчерпана, величина
убывает до тех пор, пока сохраняется возможность дальнейшего ориентирования частиц вдоль линий тока, а затем, когда такая возможность исчерпана, величина 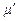 становится постоянной, а кривая течения - линейной. К псевдопластичным жидкостям относятся растворы и расплавы высокополимеров.
становится постоянной, а кривая течения - линейной. К псевдопластичным жидкостям относятся растворы и расплавы высокополимеров.

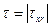
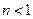
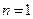
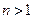
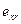
Рис. 11.2.Кривые течения степенных жидкости
Свойствами дилатантности обладают, суспензии с большим содержанием твердой фазы. Рейнольдс, открывший это явление, предположил, что в состоянии покоя такие суспензии имеют минимальный объем прослоек между твердыми частицами, поэтому жидкости достаточно только для заполнения прослоек. При течении суспензии с малой скоростью сдвига, жидкость служит смазкой и касательные напряжения трения невелики. Однако при увеличении скорости сдвига плотная упаковка частиц нарушается, и жидкости становится недостаточно для смазки трущихся друг о друга частиц, поэтому действующие напряжения значительно увеличиваются. Существуют, однако, и другие среды, как, например, крахмальные пасты, которые не относятся к суспензиям и не расширяются при сдвиге, но, тем не менее, обнаруживают дилатансию.
Отметим, что индекс 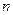 течения для многих сред является постоянным в достаточно широком диапазоне скоростей сдвига, однако, существуют и такие среды, для которых одного и того же значения
течения для многих сред является постоянным в достаточно широком диапазоне скоростей сдвига, однако, существуют и такие среды, для которых одного и того же значения 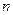 для всего диапазона скоростей сдвига подобрать нельзя. В подобных случаях весь диапазон скоростей сдвига разбивают на отдельные интервалы, в каждом из которых индекс течения считают постоянным. Индекс
для всего диапазона скоростей сдвига подобрать нельзя. В подобных случаях весь диапазон скоростей сдвига разбивают на отдельные интервалы, в каждом из которых индекс течения считают постоянным. Индекс 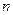 течения безразмерен; размерность консистентности k зависит от значения n.
течения безразмерен; размерность консистентности k зависит от значения n.
в) Жидкости с реологическими характеристиками, зависящими от времени. Для этих жидкостей весьма существенен фактор времени и так называемая механическая предыстория вещества. В зависимости от продолжительности предшествующей деформации величина 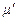 кажущейся вязкости либо уменьшается (тиксотропия), либо увеличивается (реопексия).
кажущейся вязкости либо уменьшается (тиксотропия), либо увеличивается (реопексия).
Тиксотропным материалам свойственно разрушение структуры под действием сдвига. Примерами тиксотропных сред служат буровые жидкости, глинистые промывочные растворы, типографские краски. Тиксотропные эффекты весьма существенны во многих практических приложениях, однако модели, досточно адекватно описывающие поведение таких жидкостей, до сих пор отсутствуют. В бурении, например, глинистые растворы рассматривают как нелинейно–вязкие жидкости или вязкопластичные жидкости, подразумевая при этом, что константы реологической модели могут изменяться в зависимости от направления процесса – нагружения или разгрузки, поэтому тиксотропные жидкости на кривых течения имеют гистерезисные петли (рис.11.3).
Жидкости, которые можно было бы отнести к категории реопексичных, встречаются на практике довольно редко. Материалы, обнаруживающие структурообразование при сдвиге –это, например, суспензии гипса, водные растворы бентонита и т.д. Реопексия обнаруживается лишь при небольших скоростях сдвига. Например, водный раствор гипса в пробирке затвердевает через 40 мин покоя. Медленно вращая пробирку вокург ее оси, можно добиться, чтобы время затвердевания сократилоь до 20 с. По всей видимости, небольшие перемещения сдвигового характера, способствуют образованию структуры, в то время как значительные сдвиги (встряхивание) разрушают ее. Кривая течения реопексичных жидкостей представлена на рис. 11.4.
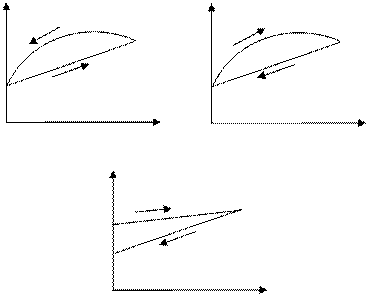
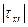
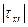
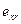
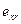
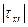
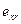
Рис. 11.3.Кривые течения тиксотропных жидкостей
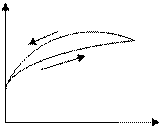
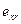
Рис. 11.4.Кривые течения реопексичных жидкостей
г) Вязкоупругие жидкости. Существуют текучие среды, которые обладают как свойствами вязкой жидкости, так свойствами упругого тела. К числу таких сред относятся очень вязкие материалы, например, смола, а также некоторые полимеры. Если напряжения в материале увеличивается постепенно, то такой материал течет как обычная вязкая жидкость; если же напряжения возрастают быстро, то возникающие деформации пропорциональны напряжениям и полностью исчезают, когда нагрузки снимются, т.е. материал ведет себя как упругое тело.
Для описания поведения вязкоупругих жидкостей известна модель Максвелла. Для чисто сдвиговой деформации (материал течет вдоль оси 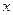 , параллельной стенкам круглой трубы;
, параллельной стенкам круглой трубы; 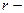 радиальная координата) реологическое уравнение этой модели имеет вид:
радиальная координата) реологическое уравнение этой модели имеет вид:
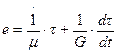 , (11.2)
, (11.2)
где 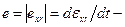 скорость деформации
скорость деформации 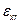 ;
; 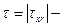 величина сдвигового напряжения; G – модуль сдвига;
величина сдвигового напряжения; G – модуль сдвига; 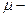 вязкость. Если
вязкость. Если 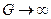 , то модель (11.2) переходит в модель ньютоновской вязкой жидкости (
, то модель (11.2) переходит в модель ньютоновской вязкой жидкости ( 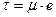 ), если
), если 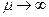 , то модель (11.2) переходит в модель упругого тела (
, то модель (11.2) переходит в модель упругого тела ( 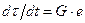 ; откуда с учетом условия
; откуда с учетом условия 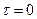 , если
, если 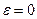 , следует, что
, следует, что 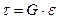 ).
).
Если положить 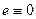 , т.е. заморозить деформацию, и проинтегрировать уравнение (11.2) по времени с начальным условием
, т.е. заморозить деформацию, и проинтегрировать уравнение (11.2) по времени с начальным условием 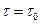 при t = 0, получим закон уменьшения касательного напряжения:
при t = 0, получим закон уменьшения касательного напряжения:
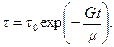 (11.3)
(11.3)
Это означает, что с течением времени касательное напряжение в жидкости возвращается к начальному значению, соответствующему равновесному состоянию, в котором скорость деформации отсутствует. Процесс возвращения к равновесному состоянию называется релаксацией, Убывание напряжения в вязко-упругой жидкости Максвелла, выражающееся уравнением (11.3), дает пример такой релаксации.
Если ввести параметр 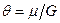 , имеющий размерности времени, то
, имеющий размерности времени, то
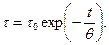
Это означает, что через каждый промежуток времени 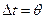 величина напряжения уменьшится в
величина напряжения уменьшится в 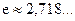 раз, поэтому параметр
раз, поэтому параметр 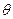 называют временем релаксации (или периодом релаксации).
называют временем релаксации (или периодом релаксации).
Вязкоупругие жидкости отличаются от вязких жидкостей не только наличием релаксационных эффектов, вызванных упругостью. В вязкоупругих жидкостях кроме касательных напряжений возникают также нормальные напряжения, перпендикулярные линиям тока. Так, например, при напорном течении жидкости в канале действие нормальных напряжений проявляется в поперечном утолщении струи сразу же после ее выхода из канала. С подобным разбуханием струи приходится считаться в ряде промышленных процессов, таких, как выдавливание волокон из фильеры, экструзионное производство пленок и труб, прокатка листового металла и т.д.
