Теоретические сведения. Метод простой итерации

Метод простой итерации. Простейшим итерационным методом решения СЛАУ является метод простой итерации.

Рассмотрим систему линейных алгебраических уравнений

,

,

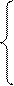
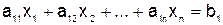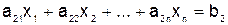……………………………… (5.1)

.

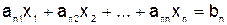Приведём систему (5.1) к виду

,

,

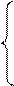
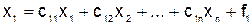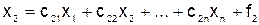……………………………………. (5.2)

.

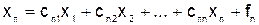В матричном виде систему (5.2) можно записать следующим образом:

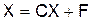, (5.3)

где

, , .

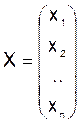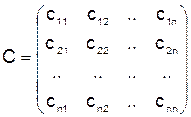За нулевое приближение решения системы возьмём произвольный вектор

.

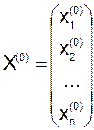Строим векторы 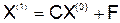, 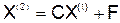и т.д., получается итерационная последовательность векторов , .

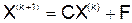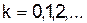Таким образом, методом простой итерации приближение 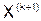вычисляется по предыдущему приближению 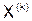путём подстановки компонент 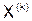в правую часть уравнений системы (5.2):

; ; .

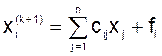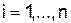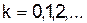Доказано, что если последовательность векторов 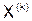имеет предел при 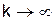, то этот предел является решением системы (5.3).

Достаточным условием сходимости метода простой итерации является условие того, что любая согласованная норма матрицы 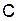должна быть меньше единицы. Отсюда с учётом наиболее применимых норм матрицы вытекает следствие.

Следствие. Для того, чтобы метод простой итерации для системы уравнений 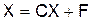сходился, достаточно, чтобы выполнялось одно из условий:

; ;

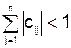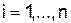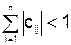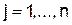; ; (5.4)

.

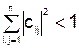На практике обычно используется первое или второе условие. Неравенства будут выполнены, если модули диагональных элементов для каждого уравнения исходной системы (5.1) больше суммы модулей всех остальных коэффициентов (не считая свободных членов). Подчеркнем, что условие является достаточным, но не является необходимым. Иными словами, существуют системы, для которых это условие не выполняется, но итерационный процесс все равно сходится.

Начальный вектор 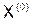можно выбрать, вообще говоря, произвольно. Иногда берут 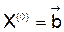. Однако наиболее целесообразно в качестве начального приближения взять приближенные значения неизвестных, полученных грубой прикидкой.

Для достижения заданной точности 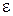итерации продолжают до тех пор, пока не выполнится условие

, .

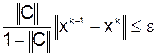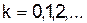Метод Зейделя. Пусть система линейных алгебраических уравнений приведена в виду (5.2). Метод Зейделя отличается от метода простой итерации тем, что при вычислении 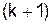-го приближения для компоненты 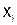учитываются определённые ранее 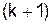-е приближения для компонент , , … , .

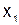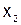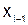Вычисления проводятся по таким формулам:

;

;

…………………………….……..……………………….

.

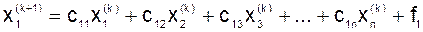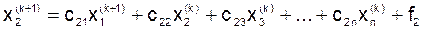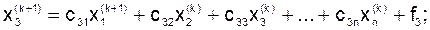
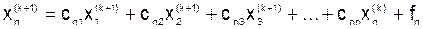Таким образом, в общем виде

, , .

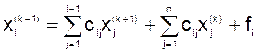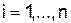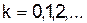Для сходимости метода Зейделя достаточно, чтобы выполнялось одно из условий:

, ;

, .

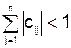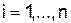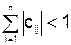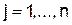Рекомендации к применению метода Зейделя остаются теми же, что и для метода простой итерации.

Приведение системы линейных алгебраических уравнений к виду, удобному для итераций. Пусть задана система линейных алгебраических уравнений (5.1) Требуется привести её к виду, удобному для итераций. Система очень просто преобразуется в случае, если модуль диагональных элементов матрицы 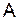, составленной из коэффициентов при неизвестных, больше, чем сумма модулей остальных элементов. Пусть выполняются приведенные ниже неравенства:

;

;

.

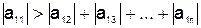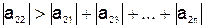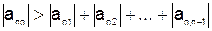Делим каждое уравнение системы (5.1) на диагональный элемент 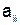( 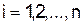) и находим 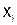( 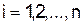), т.е. решаем первое уравнение относительно 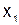, второе – относительно 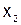и т.д. Легко проверить, что полученная таким образом система уравнений удовлетворяет первому условию (5.4). Таким образом, выполняется достаточное условие сходимости методов простой итерации и Зейделя.

Если же диагональные элементы матрицы 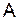не преобладают над остальными элементами, можно поступить следующим образом. Из заданной системы выделяем уравнения с коэффициентами, модули которых больше суммы модулей остальных коэффициентов уравнения. Выделенные уравнения вписываем в ту строку новой системы, в которой бы наибольший по модулю коэффициент оказался диагональным. Из неиспользованных и выделенных уравнений системы образуем линейные комбинации для составления недостающих уравнений, причем диагональные коэффициенты по модулю должны быть больше суммы модулей остальных коэффициентов. Необходимо следить, чтобы при составлении новой системы использовалось каждое уравнение заданной системы. Полученная таким образом система имеет матрицу с диагональными доминирующими элементами, и достаточное условие сходимости итерационного процесса выполняется.