Точки разрыва функции и их классификация

Если условия непрерывности функции в точке x₀ не выполнены,
т. е. в точке x₀ существует конечный предел, не равный значению функции в этой точке, либо равный бесконечности, либо вообще не существует, то говорят, что функция имеет разрыв в этой точке.

Различают точки разрыва первого рода и точки разрыва второго рода. Если функция в точке x₀ имеет конечные пределы слева и справа, из которых хотя бы один не равен f(x₀), то точка x₀ называется точкой разрыва первого рода функции f(x), а величина 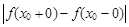– скачком функции в точке x₀. Если при этом 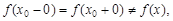то точка x₀ называется устранимой точкой разрыва функции f(x), так как, заменяя ее значение x₀ в точке x₀ общим значением 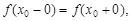получим непрерывную функцию.

Если хотя бы один из односторонних пределов 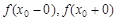равен бесконечности или не существует, то x₀ называется точкой разрыва второго рода функции f(x).

Пример 4. Функция f(x)= 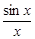при x ≠ 0 непрерывна как отношение двух непрерывных функций. Полагая f(0) = 1 в соответствии с пределом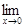 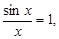получим функцию f(x)= 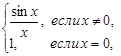непрерывную и в точке x = 0.

Пример 5. Исследовать на непрерывность функцию f(x)=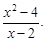

Решение

Функция элементарная, определена и непрерывна на всем множестве действительных чисел, за исключением точки x = 2. В этой точке функция имеет разрыв. Найдем предел 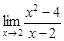= 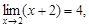отсюда f(2 + 0) = f(2 – 0) = 4.

Таким образом, в точке x = 2 функция имеет устранимый разрыв 9 (рисунок 28). Если эту функцию доопределить в точке x = 2, положив f(2) = 4, то она будет непрерывной на всей числовой прямой. В этом случае говорят, что функцию f(x) доопределили по непрерывности в точке x = 2.

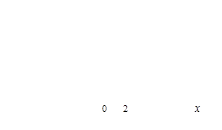
Рисунок 28

Пример 6.Исследовать на непрерывность функцию

f(x) =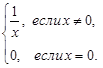

Решение

Функция имеет разрыв второго рода в точке x = 0 с обеих сторон, так как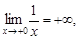

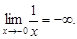
Тест 7. Функция f(x) =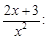

1) имеет разрыв первого рода;

2) имеет разрыв второго рода;

3) является непрерывной.

Тест 8. Функция f(x) =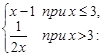

1) имеет разрыв первого рода;

2) имеет разрыв второго рода;

3) является непрерывной.

Тест 9. Функция f(x) =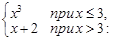

1) имеет разрыв первого рода;

2) имеет разрыв второго рода;

3) является непрерывной.

Тест 10. Функция f(x) = 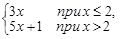в точке x = 2:

1) имеет устранимый разрыв первого рода;

2) имеет разрыв первого рода;

3) имеет разрыв второго рода;

4) является непрерывной.

Тест 11. Функция f(x) = 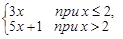в точке x = 0:

1) имеет устранимый разрыв первого рода;

2) имеет устранимый разрыв второго рода;

3) имеет разрыв второго рода;

4) является непрерывной.

Рассмотрим свойства функций, непрерывных в точке:

1. Если функции f(x) и g(x) непрерывны в точке х₀, то их алгебраическая сумма f(x) + g(x), произведение f(x) × g(x) и частное f(x) / g(x) (при условии g(x) ≠ 0) являются функциями, непрерывными в точке х₀.

2. Если функция y = f(x) непрерывна в точке х₀ и f(х₀) > 0, то существует такая окрестность точки х₀, в которой f(x) > 0.

3. Если функция y = f(u) непрерывна в точке u₀, а функция u = j(x) – в точке х₀, 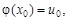то сложная функция y = f(φ(x)) непрерывна в точке х₀.

Функция y = f(x) называется непрерывной на множестве М, если она непрерывна в каждой точке этого множества. Все элементарные функции непрерывны в области их определения.

Функция y = f(x) называется непрерывной на отрезке [a; b], если она непрерывна в каждой внутренней точке отрезка (a < x < b) и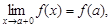

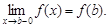
Рассмотрим свойства функций, непрерывных на отрезке:

1. Если функция y = f(x) непрерывна на отрезке, то она ограничена на этом отрезке.

2. Теорема Вейерштрасса: если функция y = f(x) непрерывна на отрезке [a; b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения М.

3. Теорема Больцано-Коши: если функция y = f(x) непрерывна на отрезке [a; b] и принимает на его концах значения противоположных знаков, то для некоторого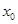

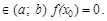
Тест 12. Функция f(x) = 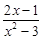является непрерывной на отрезке:

1) [–5; 0];

2) [0; 5];

3) [–2; 2];

4) [1; 10];

5) имеет разрыв на каждом из указанных отрезков.

Тест 13. Функция f(x) = 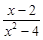является непрерывной на отрезке:

1) [–5; 0];

2) [0; 5];

3) [–1; 0];

4) [1; 10].

Тест 14. Функция f(x) = 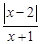является непрерывной на отрезке:

1) [–5; 0];

2) [2; 5];

3) [–2; 0];

4) [–10; 10].

Тест 15. Функция f(x) = 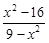является непрерывной на отрезке:

1) [–5; 0];

2) [0; 5];

3) [–5; 5];

4) [5; 9].

Ответы на тестовые задания

Номер теста
Правильный ответ

Номер теста
Правильный ответ