Введение в математический анализ

В.В. Астраханцев,

Б.Ф. Сковорода

Редактор В. И. Варламов

Методические указания содержат 4 контрольные работы по высшей математике для студентов 1 курса заочного факультета ИГЭУ:

1 семестр – контрольные работы № 1 и 2,

2 семестр – контрольные работы № 3 и 4.

Приводятся программа по курсу высшей математики для 1 и 2 семестров и указания к выполнению контрольных работ № 1 − 4.

Утверждены цикловой методической комиссией ИВТФ.

Рецензент

кафедра высшей математики Ивановского государственного энергетического университета.

Рекомендации по выполнению и оформлению контрольных

работ

При выполнении контрольных работ необходимо учитывать указанные ниже рекомендации. Работы, выполненные без соблюдения этих рекомендаций, не зачитываются и возвращаются студенту для переработки.

1. Каждая контрольная работа должна быть выполнена в отдельной тетради в клетку. Необходимо оставлять поля шириной 425 см для замечаний рецензента.

2. На обложке тетради должны быть написаны фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины; здесь же указывается название учебного заведения, дата отсылки работы и адрес студента. В конце работы ставится дата ее выполнения и подпись студента.

3. В работу должны быть включены все задачи, указанные в задании по положенному варианту. Контрольные работы, содержащие не все задачи задания, а также задачи не своего варианта, не зачитываются.

4. Решения задач следует располагать в порядке номеров, указанных в задании, сохраняя номера задач, излагать подробно, объясняя и мотивируя все действия по ходу решения.

5. Перед решением каждой задачи надо полностью выписать ее условие. Если несколько задач, из которых нужно выбрать задачи варианта, имеют общую формулировку, то следует, переписывая условие задачи, заменить общие данные конкретными, взятыми из соответствующего номера.

6. После получения прорецензированной работы, студент должен исправить все отмеченные рецензентом ошибки и выполнить все его рекомендации. Внесенные в решения задач исправления или дополнения следует прислать для повторной проверки. Если работа не зачтена и отсутствует указание рецензента на то, что можно ограничиться представлением исправленных решений отдельных задач, то вся работа должна быть выполнена заново.

При выполнении контрольной работы рекомендуется оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений. Вносить исправления в сам текст работы после ее рецензирования запрещается.

Внимание!В каждой контрольной работе вам нужно решить задачи, последняя цифра номера которых совпадает с последней цифрой вашего шифра. Так, например, если ваш шифр оканчивается цифрой 3, то в контрольной работе №1 вам нужно решить задачи № 3, 13, 23, 33, 43 и 53.

Программа по высшей математике для ФЗВО (1, 2 семестры)

Векторная алгебра

Координаты, модуль, направляющие косинусы вектора. Скалярное, векторное и смешанное произведение: определение и вычисление. Угол между векторами. Признаки параллельности и перпендикулярности векторов. Площадь параллелограмма и треугольника. Объем пирамиды, построенной на векторах. Признак компланарности векторов.

Аналитическая геометрия на плоскости

Различные виды уравнений прямой на плоскости. Угол между прямыми. Признаки параллельности и перпендикулярности прямых.

Уравнение окружности. Эллипс, гипербола, парабола (определение, канонические уравнения). Параллельный перенос системы координат. Полярные координаты и их связь с декартовыми.

Аналитическая геометрия в пространстве

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение плоскости. Канонические и общие уравнения прямой. Угол между плоскостями, прямыми, прямой и плоскостью. Признаки параллельности и перпендикулярности плоскостей, прямых, прямой и плоскости.

Элементы линейной алгебры

Матрицы, определители, системы. Действия над матрицами. Обратная матрица. Решение системы линейных уравнений методом Гаусса, по формулам Крамера и матричным способом.

Линейные преобразования векторов в пространстве и на плоскости. Нахождение собственных чисел и собственных векторов матрицы.

Комплексные числа

Определение комплексного числа. Изображение на плоскости. Алгебраическая, тригонометрическая, показательная формы. Действия над комплексными числами. Формулы Муавра и Эйлера. Извлечение корня из комплексного числа. Логарифм комплексного числа. Возведение комплексного числа в комплексную степень.

Введение в математический анализ

Предел последовательности. Предел функции. 1-й и 2-й замечательные пределы. Раскрытие неопределенностей вида

, , , , .

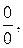
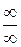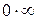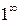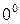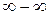Непрерывность функции. Точка разрыва. Односторонние пределы.