Д5.1 Правило дифференцирования. Производная суммы, разности, произведения и частного функций
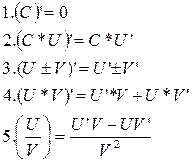 | ||||
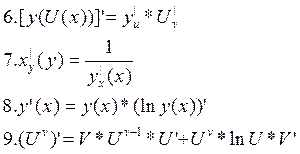 | ||||
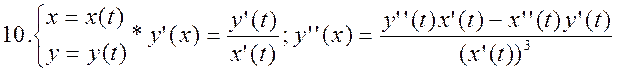 |
Д5.2 Производная обратной функции.
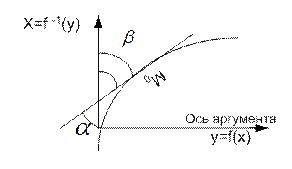 Пусть у=f(x) в точке x0. Если существует х=f-1(y) тогда она имеет производную в точке y0=f(x0), прямой
Пусть у=f(x) в точке x0. Если существует х=f-1(y) тогда она имеет производную в точке y0=f(x0), прямой 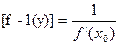
y=f(x)
x=f -1(y)
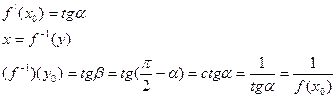
Д5.3 Производная сложной функции.
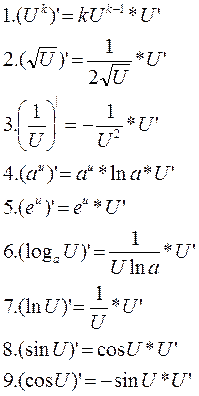 | 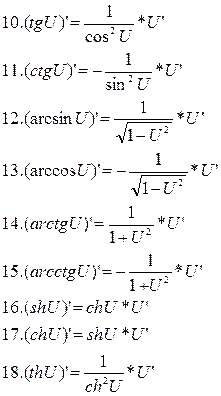 |
Д6.1 Понятие обратной функции, функции заданной неявно и параметрически.
Пусть функция y=f(x) определена на X и Y-множество ее значений. Если каждому значению y из Y(y 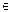 Y) по тому же самому закону ставится в соответствие единичныый элемент x
Y) по тому же самому закону ставится в соответствие единичныый элемент x 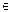 X то говорят, что на множестве Y определена обратная функция y=f(x). Графики прямая и обратной функции совпадают. Не для всякой функции можно определять обратную функцию.
X то говорят, что на множестве Y определена обратная функция y=f(x). Графики прямая и обратной функции совпадают. Не для всякой функции можно определять обратную функцию.
Т)Если функция y=f(x) строго монотонна и непрерывна на множестве X то на множестве ее значений Y существует обратная функции x=f -1(y)
y(x)=x2, x 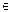 [0,+
[0,+ 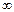 ]; y=x2- строго возраст и непрерывна, как элементарная функция на [0,+
]; y=x2- строго возраст и непрерывна, как элементарная функция на [0,+  ]. Следовательно на Y=[0,+
]. Следовательно на Y=[0,+  ] существует обратная функция x=y1/2. Геометрически этому преобразованию отвечает симметричное отображение графика f(x) относительно биссектрисе 1 и 3-го координатных углов.
] существует обратная функция x=y1/2. Геометрически этому преобразованию отвечает симметричное отображение графика f(x) относительно биссектрисе 1 и 3-го координатных углов.
Зам-е)Условия строгой монотонности и непрерывности функции y=f(x) является существенными для существования обратной функции.
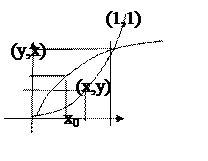
Опр. Функция y=f(x) называется неявной функцией независимой переменной х, если она задана уравнением F(x;y)=0, не разрешаемой относительно y.
При подстановке y=f(x) в равенство F(x;y)=0 вместо у оно обращается в тождество, т.е. F(x;f(x))≡0.
Параметрически заданная функция.
Пусть на интервале (α,β) заданы 2 функции x=x(t) и y=y(t). И пусть x=x(t) строго монотонна и непрерывна на (α,β). Тогда на множестве ее значений существует обрат функция t=t(x).Подставим ее в y=y(t), получим y=y[t(x)]
Функция y=y[t(x)] заданная с помощью уравнений y=y(t) и x=x(t) t 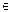 (α,β) называется заданной параметрически.
(α,β) называется заданной параметрически.
Д6.2 Дифференцирование неявно заданной функции; функции, заданной параметрически.
F(x,y) y|x -?
Если зависимость между аргументом x и функцией этого аргумента у задана уравнением, неразрешенном относительно у, то для отыскания производной от y по x надо продифференцировать этого уравнения по х, рассматривая при этом у как функцию от х. разрешая полученное уравнение (х, у, х’, y’) относительноy’. Найдем у’ по х.
Параметрически.
Пусть зависимость между аргументом х и функцией задана параметрически
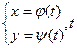 - параметр
- параметр
Д6.3 Логарифмическое дифференцирование
Если y=y(x)>0 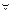 x
x 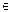 X и функция y(x) упрощается после логарифмирования то целесообразно сначала найти lny(x), а затем используя правило дифференцирования неявно заданной функции найти y’(x)
X и функция y(x) упрощается после логарифмирования то целесообразно сначала найти lny(x), а затем используя правило дифференцирования неявно заданной функции найти y’(x)
1) y=U(x)V(x), U(x)>0 (показательно степенная)
(lny)’x=(V(x)lnU)’x (неявно заданная функция)
(1/y(x))*y’(x)=V’(x)lnU(x)+V(x)*(1/U(x))*U’(x)
y’(x)=U(x)V(x)*[V’(x)lnU(x)+V(x)*U’(x)/U(x)]
