Свойства силовских подгрупп

Лемма 2.3.1 (Фраттини).Пусть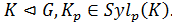

Тогда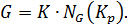

Доказательство.

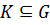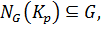1) Так как и то .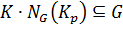

2) Покажем, что 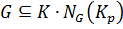.Пусть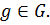

Рассмотрим 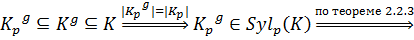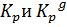сопряжены в 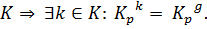Следовательно, 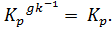Тогда 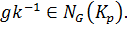Таким образом, 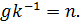Соответственно, 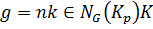. Следовательно, .

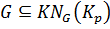Из 1) и 2) получим 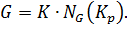Лемма доказана.

Лемма 2.3.2 Пусть 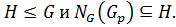Тогда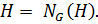

Доказательство. Пусть 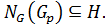Покажем, что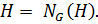

1) С одной стороны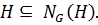

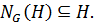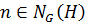2) Покажем, что Пусть . Покажем, что .

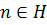Рассмотрим :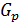

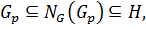
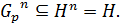
Таким образом, 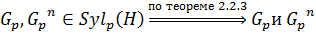сопряжены в 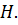Следовательно, 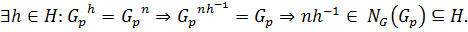Тогда 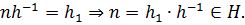Таким образом, 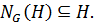Лемма доказана.

Теорема 2.3.1 Пусть 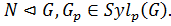Тогда справедливы следующие утверждения:

1)

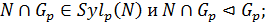
2)

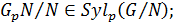
3)

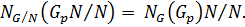
Бипримарные группы

Определение 2.4.1. Группа G называется бипримарной, если 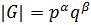, где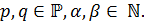

Теорема 2.4.1(Бернсайда). Конечная бипримарная группа является разрешимой.

Следствие 2.4.1. Группа порядка 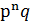разрешима для любого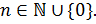

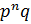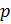Теорема 2.4.2 Пусть ‒ группа порядка , где и 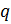‒ различные простые числа. Тогда:

1) если 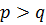, то силовская 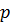-подгруппа нормальна в ;

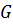2) если 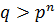, то силовская 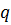-подгруппа нормальна в ;

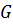3) если 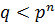, но , то в группе 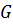есть неединичная нормальная 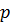-подгруппа.

Доказательство. Пусть 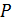и 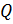‒ силовские 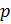-подгруппа и 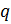-подгруппа группы . Ясно, что 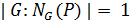или 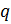, а по теореме Силова

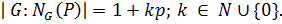
Аналогично,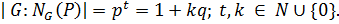

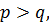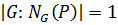1) Если то и 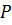‒ нормальная подгруппа группы .

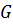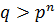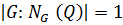2) Если , то и 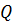‒ нормальная подгруппа группы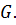

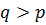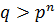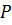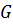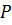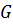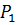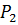3) Теперь пусть и . Если ‒ нормальная подгруппа группы , то утверждение (3) справедливо. Пусть не является нормальной подгруппой группы и пусть и ‒ различные силовские 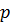-подгруппы группы 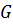, для которых пересечение 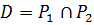имеет наибольший порядок. Так как

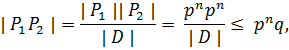
то 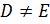. Если 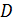‒ нормальная подгруппа группы , то теорема доказана.

Пусть 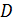не является нормальной подгруппой группы . Подгруппа 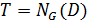не является 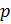-группой, поэтому некоторая силовская 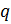-подгруппа 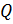группы содержится в 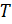. Так как 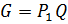, то каждый элемент 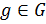представим в ви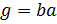де , где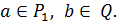

Поэтому 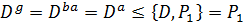. Теорема доказана.

Заключение

В данном реферате были выполнены следующие задачи:

§ Рассмотрены основные определения теории групп (определение абелевой группы, порядка группы, правого и левого смежного классов, индекса подгруппы, минимальной и максимальной нормальной подгруппы, понятия нормализатора и централизатора, примарной и бипримарной групп и другие).

§ Проведено исследование свойств примарных группы. Рассмотрено определение силовской 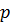-подгруппы конечной группы и изучены свойства силовских 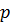-подгрупп.

§ Исследованы основные теоремы Силова: о существовании силовских p-подгрупп; о сопряженности силовских p-подгрупп и вложении p-подгруппы в силовскую p-подгруппу; о числе силовских p-подгрупп.

§ Исследованы бипримарные группы и их основные свойства.

Список литературы

1. Воробьев Н.Н. Алгебра классов конечных групп. Витебск: ВГУ имени П.М. Машерова, 2012.

2. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. - М.: Наука, 1982.

3. Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры. - М.: Физико-математическая литература, 2000.

4. Кострикин А.И. Введение в алгебру. Часть 2. Линейная алгебра. - М.: Физико-математическая литература, 2000.

5. Кострикин А.И. Введение в алгебру. Часть 3. Основные структуры алгебры. - М.: Физико-математическая литература, 2000.

6. Курош А.Г. Теория групп. – М.: Физико-математическая литература, 2011.

7. Монахов В.С. Введение в теорию конечных групп и их классов: учебное пособие. – Мн.: Вышэйшая школа, 2006.